4.7.3 自注意力网络(Transformer)
自注意力网络(Transformer) 是一种基于自注意力机制(Self-Attention)的深度神经网络结构分类。最初的设计原型来自于 2015 年由 约书亚·本吉奥(Yoshua Bengio,1964~Present) 有关神经网络翻译模型优化而提出的设想 [22] 。
本吉奥 通过引入一种模拟生物在感知、学习、思考过程中自然而然产生的,主被动关注关键点的生理机制,来解决传统 机器学习(ML)编码器-解码器(Encoder-Decoder) 翻译模型(Translation Models)的 长句压缩固定长度(Fixed-Length) 特征,导致潜层语意缺失的问题。这种模拟方式,能够将长句(Long Sequence)中的信息,抽象为固定长度(Fixed-Length)向量的集合,而非 以单一向量的形式进行后续相关语意分解工作。
基于该研究,Google AI 实验室终于在 2017 年以 《Attention Is All You Need》[23] 一文,确定了基本的网络结构设计。 从此,开启了 Transformer 类型网络的快速发展之路。
Transformer 核心成分 & 核心机制
自注意力机制(Self-Attention) 是 Transformer 的 核心机制。而 Transformer 网络结构,则是与自注意力机制提取特征 配套,用于达成转译目的(不一定非要是语言)的整个编解码器 系统作业流水线。
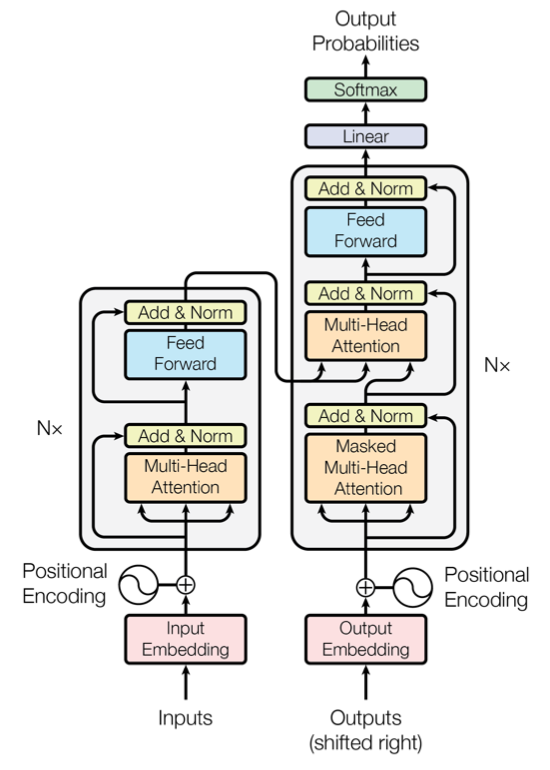
图 4-49 Transformer 网络结构 [23]
Transformer 在结构中,参考了 RNN 和早期 自编解码网络系统的特点,采用 时序上以串行元胞(Cell),而单次迭代中编解码(Encoder-Decoder)并行(Parallelization) 的方式,结合两者各自所长。
如此设计的原因,一方面来自于 Transformer 意图改善 RNN 对 序列到序列(Seq2Seq) 任务的处理能力。这便要求,其本身对输入样本的高级特征提取,能够拆解直接关联性,但却又可以保留更高维度潜藏的逻辑信息。另一方面,注意力机制只能提炼解构关联性特征,但我们需要的结果却是对原有输入的另一种未改变原意的表述,决定了必须有编解码类似的结构(至少目前为止)对高级特征进行非对称的压缩和还原。
自注意力机制,保证了前一点。整体结构,保证了后一点。而 注意力单元(Attention Unit),则是用于完成自注意力处理的组成框架的一部分(图中橙色)。
根据最精简实现,
从 注意力单元(Attention Unit) 上,Transformer 包括了两个分步主成分:
- 放缩点积注意力(SDPA),用于完成对于一次 Transformer 输入的单一注意力筛选;
- 多头注意力(MHA),通过对放缩点积的平行组合,完成对同一输入的多点注意力检测;
从 网络结构(Network Structure) 上,Transformer 包括了两个主体模块:
- 编码器(Encoder)模块,用于完成对样本输入的高级特征提取;
- 解码器(Decoder)模块,用于完成对样本输入的转译结果输出;
通俗来说,以人做类比,两者一个属于 Transformer 的“灵魂”,一个属于 Transformer 的“身躯”。从宏观角度,是互为一体的存在。这与前两节 CNN 、RNN 里,结构占相对主导地位(即框架为改进的关键)的情况有所不同。而是皆有突破。
正是这样,Transformer 才称为深度学习领域,在模型结构基本方法论上,近年来相对具有较大革新突破的工具。
刚刚我们提到的注意力单元,是对自注意力机制的实现。从上可知,Transformer 基本的一切都是围绕其运转的。那么,什么是自注意力机制(Self-Attention)呢?
自注意力机制(Self-Attention)
自注意力机制(Self-Attention) 是 Transformer 中,一种目的用于模拟生物注意力的数学量化范式。是 一类方法的方法论。
想要能够区分轻重,最容易想到的方式便是加权了。因此,在 Transformer 中,对注意力的数值定义便是:
对输入序列元素,根据输入查询元素键值对,以求动态计算加权平均值的权重。
所以,我们计算注意力,需要的输入数据序列就必须包含三个重要的信息维度,分别是:
- 查询信息,即查询(Query),代表当前输入具有可能被关注(查询)的意义表征;
- 关键信息,即键值(Keys),代表当前输入在查询(Query)下可能提供的信息特征;
- 标值信息,即取值(Values),代表与键值(Key)关联的量化查询积分;
最终,由三者共同借由算法组成 输出特征(Output Fratures),即 加权平均值的权重,作为 Transformer 的神经网络内高级特征。
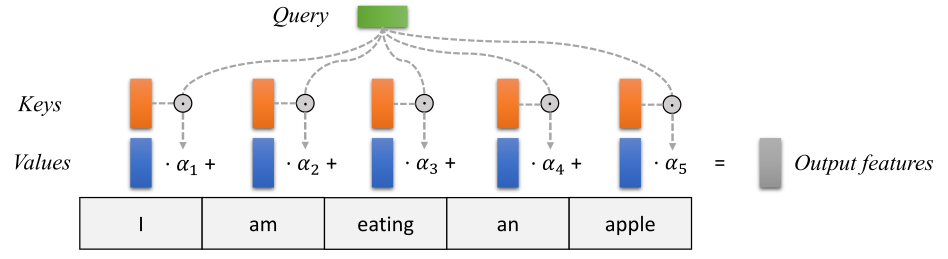
图 4-50 Transformer 的输入转换过程 [23]
显然,虽然键值和取值可以按照 传统键值对(Key-Value Pair) 形式直接配对(当然也可以有复杂映射实现)。但从查询到键值还需要有一定转换方式,通过它来实现将查询可能的关注点,分散到对应的键值上,从而构成可以计算的结果。这个转换方式,就是 评分函数(Score Function)。
一般而言,评分函数可分为两类:
- 简单评分函数(Simple Scorer),此类以单步函数来完成粗糙的映射,如直接 Sigmod
- 复杂评分函数(Complex Scorer),此类用朴素神经网络或模型来完成映射,如 MLP 评分
而现有大部分 Transformer 中,采用的都是第二个类型的实现。包括基础 Transformer 的 SDPA 和 MHA 在内,皆属于此类。
当评分函数确定后,每个查询都能拆解到键值上,并获取对应积分了。此时,就需要由 输出函数(Output Function) 来将各个部分组合成最终的高级特征向量进行输出。
假设,
- 以 代表查询,
- 以 表示输入序列,
- 以角标 代表所处输入序列 的位置,有 处键值 取积分 ,
- 以 代表经过注意力筛选后,的高级特征向量,
- 记评分函数为 ,输出函数为
则有:
如此,我们便得到了 注意力量化公式。实际上,这种按序列计算的过程,常被直接 以矩阵运算代替。公式的意义更多在于原理描述。即,自注意力机制工程化的指导过程。依照上式,便可以通过构建评分函数和输出函数,来设计 Transformer 里的注意力单元了。
经典 Transformer 中,将这一步分为了两个组成。
放缩点积注意力(SDPA [Scaled Dot-Product Attention])
放缩点积注意力(SDPA [Scaled Dot-Product Attention]) 被用于计算单点注意力,即只生成一个注意力高级特征输出。
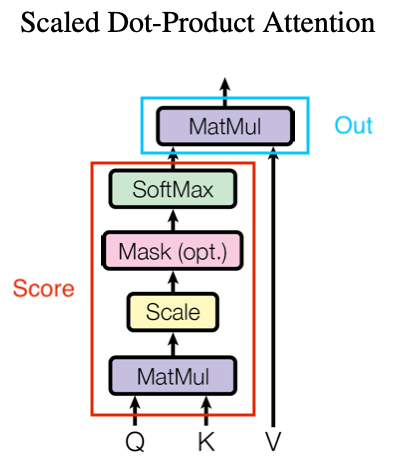
图 4-51 Transformer 的 SDPA 单元 [23]
如图,红框部分便是 SDPA 的评分函数,而蓝框部分则为 SDPA 的输出函数。
我们记一个输入序列,其序列长度为 而查询维度为 。这里需要解释一下,什么是序列长度和查询维度。我们举个例子,如果有一条查询为 ,那么我们就称 单条查询的维度 为 ,而 总共有长度 为 条查询。即 查询维度就是一条查询所包含的参数数目,而 序列长度就是单次输入样本包含查询的数目。
当 确定,对于长度 的输入数据序列,就有 查询 、 键值 、 取值 ,即三者都是 大小的矩阵。则 SDPA 的 评分函数(Score Function) 有如下表示:
而输出时采用的 输出函数(Output Function),就是一个取值与评分结果的矩阵点积(Dot-Product),这也是 SDPA 名称的原因。即:
过程中 即 缩放因子(Scale Factor)。而 Mask 操作是可选的,一般过程中作用于 的 SoftMax 操作之前,已经完成点积和缩放的 这个 大小的矩阵。通过屏蔽部分数据或进行简单过滤,来进一步加工交给 Softmax 的输入。
实际操作时,可以在 编码器(Encoder) 阶段引入 Mask 层来做 部分参数优化,加速训练。而 解码器(Decoder) 需要用 Mask 来做 零值处理。即,将 结果中的部分数据标记为 0 或极小值(如 1e-12 ,避免权重消失),组成不完整数据。
在经过一系列运算后,根据矩阵点乘的特性,最终输出为具有 的大小的 单次注意力张量(Tensor)。
不过,我们想要的是有多个关注点的高维特征,单个注意力无法满足要求。 这就需要 MHA 了。
多头注意力(MHA [Multi-Head Attention])
多头注意力(MHA [Multi-Head Attention]) 是对多个单头注意力,即放缩点积注意力(SDPA),处理的加权复合。
千万需要小心的是,正是在 MHA 中,我们引入了真正用于 持久训练 的迭代用权重参数,构成参数矩阵参与模型训练。
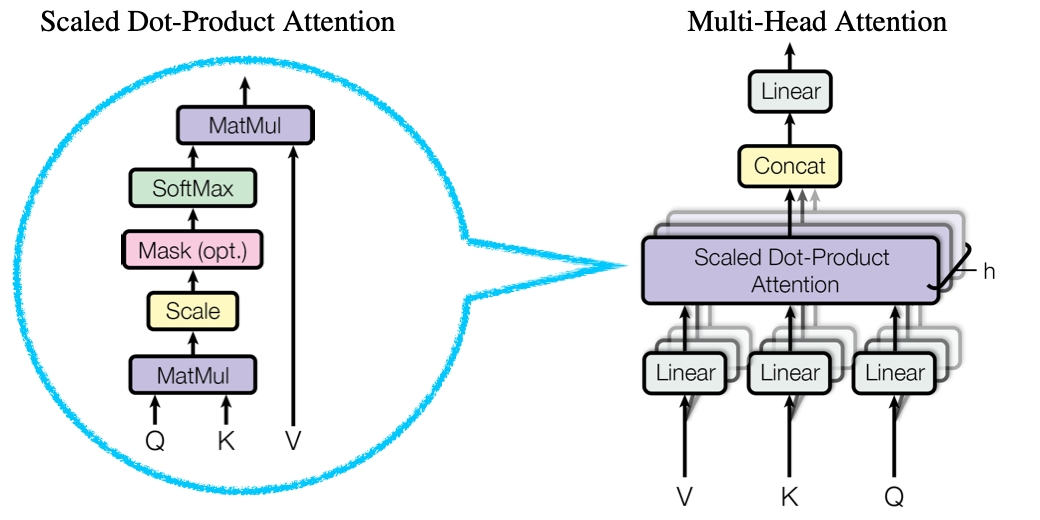
图 4-52 Transformer 的 MHA 单元与 SDPA 单元的关系
如图,蓝色气泡内便是 SDPA 单元。在图例中,由 个 SDPA 单元,经过链接层(Concat 为简写),和线性归一化(目的是为了保证输入输出等大),构成了最终 MHA 的输出。
所以,从另一个角度来看,链接层函数就相当于 MHA 的评分函数,线性归一化则是输出函数。而 MHA 真正意义上的输入,即每个 SDPA 输入的集合。有:
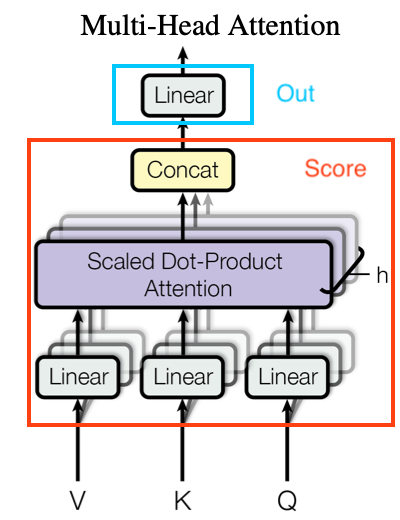
图 4-53 Transformer 的 MHA 单元 [23]
上方即为 MHA 在 Transformer 中的基本算子表示。红框部分便是 MHA 的评分函数,而蓝框部分则为 MHA 的输出函数。可见,评分函数和输出函数的概念,也是相对于被选择作为参考的单元本身而言的。
我们仍然取一个输入序列(MHA 和 SDPA 都是对同一序列的操作,仅目标输出不同),其序列长度为 而查询维度为 。
记当前一个 MHA 总共有 个 SDPA 单元,每个单元按照顺序,由角标 表示序号。则,对于顺序 的 SDPA 单元输入,有查询 、 键值 、 取值 ,即三者都是 大小的矩阵。并有经过 SDPA 处理后的输出 ,简记为 交付链接。
由于采用了多组 SDPA 组合,我们不再能以固定形式,确定每个 SDPA 输入的重要程度。因此,需要对每个构成 MHA 的 SDPA 算子的输入 进行确权,来通过训练得到实际 MHA 的输入的初始关注点。
介于这一点,我们对每一组顺序 的 SDPA 单元输入进行加权。引入 输入权重(Input Wights),根据加权对象,分为 组查询权重 、 组键值权重 、 组取值权重 。 注意,加权需要用和加权对象维度转置(Transpose)的矩阵。
加权后,顺序 的 SDPA 算子的输入就变为了 。同时,这也是为什么 MHA 中,Q、K、V 需要经过一次线性归一化。即目的是为了保证每一组的输入在样本值上的价值等同。
调整后,MHA 的 SDPA 计算公式 化为:
使得 MHA 的评分函数(Score Function)有如下表示:
其中,连接函数(Concat [Connection Function])是简单全链接。即,将每一个 SDPA 的输出 顺序拼接,构成 的输出。
而输出时采用的输出函数(Output Function),存在迭代的 目的权重(Target Wight) 矩阵 ,以权重代表注意力积分并参与训练(即动态的积分)。有:
其中,线性归一化算子(Linear) 其实同 MHA 的 SDPA 输入线性归一化一样,目的在于归一化 MHA 的输出以取得我们想要的多关注点高维特征,并同时让输出保持与输入相同的维度大小。即,通过 ,让原本 大小的数据,通过以 大小分块,分为 块叠加求均值,来使最终输出的 大小。
所以,MHA 的完整处理公式为:
至此,特征提取完毕。
由 MHA 的输出 和权重矩阵 ,参与到 Transformer 训练的内部过程。
Transformer 的辅助处理单元
在正式开始 Transformer 的网络结构讲解前。我们还需要了解一下,自注意力网络(Transformer)中的 其它辅助机制。
在经典结构中,Transformer 除了使用自注意力来完成特征提取外,还使用了由 ResNet 提出在当时已经相对成熟的 残差连接(Residual Connection) 技术,并使用简单 前馈控制(Feed Forward) 来修正 MHA 特征,提供非线性和引入深层次的 隐藏权重(Hidden Wight) 参与训练。
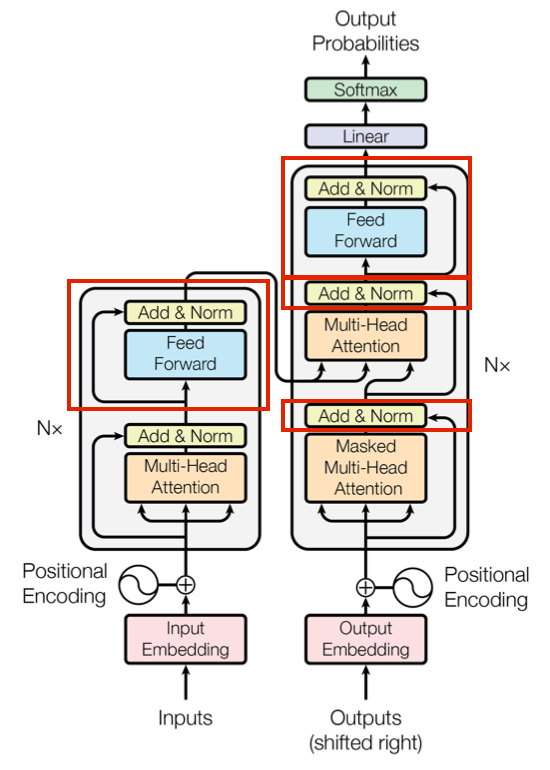
图 4-54 Transformer 辅助机制作用位置
图中红框的部分,即为这两个机制起作用的位置。一般,在 Transformer 中,将其分别称为 前馈控制单元(FFU [Feed Forward Unit]) 和 加和标准化单元(ANU [Add & Norm Unit])。
记两者的输入为 ,输出为 。
大部分情况下前馈控制单元的输入 都为 MHA 的输出,即 但也有例外。加和标准化单元则需要两个输入。不过,在这两个单元的处理中,我们为了保证输入前后特征张量(Tensor)的一致性,要求不论 FFU 还是 ANU,都必须实现输入输出大小相等。
所以,在整个 Transformer 中,FFU 和 ANU 都有 。
而两者的 驱动公式(Core Formula),则为:
每一个 FFU 都能为我们引入一套权重 和偏移 参与训练。而 ANU 则负责通过 归一化(Normalization) 将样本数据映射到一定范围区间内,保证前级输出的统一尺度衡量,加速模型收敛。
所有原件准备就绪,Transformer 网络结构就非常容易理解了。
Transformer 网络结构
在本节开始时提到,自注意力网络(Transformer)从结构角度分为编码器(Encoder)和 解码器(Decoder)。两者在整体上分别对同一个序列(Sequence)进行不同处理。
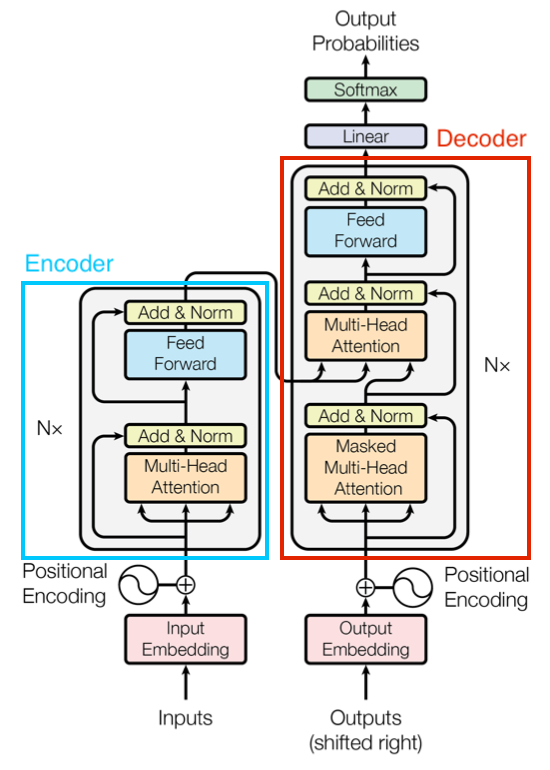
图 4-55 Transformer 编解码器示意图
如图,蓝框内部分即编码器(Encoder)的构成,红框内部分则是解码器(Decoder)。
编码器(Encoder) 接收正常顺序的序列,如:“I am eating an apple” 经过 位子编码(Positional Encoding),再以特征工程提炼出的 。
之后,交由 MHA 提取高级特征,并将提取的高级特征经过一次 ANU 归一化。最终,归一化的高级特征通过 FFU 加隐藏的核心权重和偏移,再次经由一次 ANU 归一化,完成当前时代的编码部分处理。记编码器的输出为 ,显然 有 大小。
解码器(Decoder) 接收被标记过的序列,如:“I am eating an apple” 经过标记(Shifted Right)变为 “\</s> I am eating an apple” ,再由特征工程提炼出的 输入。
标记(Shifted Right) 的作用是为了区分每一个序列的起点,例子里我们采用的是 “\</s>” ,当然也可以用其他标志。 之后,交由 加遮罩(Mask)的 MHA 提取高级特征,并 ANU 归一化。这里的 遮罩,就是前文中提到的 SDPA 的可选 Mask 操作,即解码器对 的零值处理。简单的 Mask 有:
即 只保留右上角数据,完成解码器对输入的第一次注意力操作。
接下来,解码器会接受编码器的同序列输出 ,作为一组键值 组合,并用前一级 MHA 的 ANU 归一化结果作为查询 ,合并为一组 作为第二个 MHA 的输入。
第二个 MHA 进行常规的 无 Mask 注意力过程。将第二个 MHA 的输出交由 FFU 加隐藏的核心权重和偏移。在 ANU 归一化后,作为解码器的最终输出。 记解码器的输出为 ,同样有 大小。
或许有心的读者已经注意到,在图例中,编解码器的核心流水线旁边都有一个数量标记 。这意味着每个编解码都是由 个这样的流水线构成的。目的是为了将 长序列(Long Sequence),拆分为顺序的单个 单词(Word),即 短序列(Short Sequence),顺序的输入处理。我们将编解码各自的一条完整流水线,称为 编码层(Encoding Layer) 和 解码层(Decoding Layer)。
那么,以解码器输入 “\</s> I am eating an apple” 为例。经过分割后,就变成了:
0 - "</s>"
1 - "I"
2 - "am"
3 - "eating"
4 - "an"
5 - "apple"
总共 6 个短句。分别交由 6 个解码层处理。最终的输出也按照解码层的顺序,进行顺序拼接。相当于每一个解码层的 。而拼接后的结果仍然是 。
这样既保证了模型本身的一定范围实时感知,也解放了模型本身的训练处理机能。在 2017 经典 Transformer 中,建议取 ,平衡效率。
Transformer 的输出 & 训练迭代
其实,经过之上的一系列工作,最终编码器的输出 ,还需要经过一次 线性归一化(Linear Normalization),再通过 SoftMax 输出概率预测结果 。预测 的大小为 是一组概率数组。
这个输出,才是最终参与模型迭代,用于损失函数的结果。
那么,Transformer 采用的损失函数是什么呢?
即然最终操作的对象是概率值,那么不难想到本质仍然属于分类(Classification)。 因此,Transformer 通常采用 交叉熵损失(Cross Entropy Loss)。即我们在损失函数一节中,提到过的:
同理,也可以考虑改用其他的分类项损失。
随后的过程就是深度学习网络(DNN)的通用过程了,用优化算法加速权重迭代。并持续训练,直到模型达成收敛指标。
而部署后,预测结果 所关联的词汇,就是最终输出。
Transformer 的常见场景
自注意力网络(Transformer)在诞生之后,大部分都被运用在 NLP 由其是 LLM 领域。
目前上,工业界对 Transformer 的运用已经涵盖了:
- 自然语言处理(NLP),如:文本分析(智能输入法)、机器翻译、语音助手等;
- 音视频生成,如:音乐生成、视频生成、合成编辑、自动裁剪等;
而配合其他网络结构,如 CNN 的原样本特征提取能力,Transformer 在图形处理上也被大量运用,涵盖了:
- 图像分类,如:手势识别、动作识别、人脸识别等;
- 图像分割,如:背景分离、智能抠图、轮廓融合等;
- 语义分割,如:物体分类、车辆检测等;
- 语音识别,如:文本转译、同声传录、情感分析等;
- 时序预测,如:股票分析、气象预测、医疗诊断等;
可以说,Transformer 几乎体现在各种方面。
至此,随着经典模型结构 自注意力网络(Transformer)介绍完毕,基本理论知识也完成了初步的梳理。
从下一章开始,我们将正式步入音视频处理的实践工程领域。