3.4.2 双向光流预测(BDOF [Bi-Directional Optical Flow])
双向光流预测值修正,简称 双向光流预测(BDOF [Bi-Directional Optical Flow]),最早在 H.265 的二版规格,由三星工程师以编码压缩补充手段的方式提出 [29] 。在 VVC 的初版制定过程中,贡献者们通过对算法层面的优化,提升了 BDOF 处理单元的性能。随 VVC 被采纳为 H.266 规格一起,作为标准的一部分被收录其中。
双向光流预测是以 LK 光流法的约束条件为基础,提出的一种亮度值推理算法。方法在编解码过程中以 LK 微位移假设为基,限制所有前后向预测帧(B帧)的选取,必须保持 当前帧(Current Frame) 与前后两帧在相同位置处的光流成 等大反向关系(Reverse Equality)。
通过这一联系,BDOF 在已知时间流向(即视频向前、向后)时,可以通过前向帧和期望预测方向的下一个关联帧,推导出当前帧的实际光流场变化情况。进而在无保存当前帧数据的前提下,求得当前帧的实际灰度值(亮度参考值)。
对于采用具有线性色彩空间映射关系的规格,依赖线性转换保证了关于灰度的推理,这时 BDOF 也可以适用在各自的原色格式(RGB)的数据通道上。但由于视频传输中,一般不直接采用会造成大量数据浪费的原色格式,所以,BDOF 只被用来对传输格式(YUV)代表亮度值的 Y 通道数据,进行冗余控制。
本质上,双向光流预测是个类似二次牛顿法的逼近求解过程。根据镜像的特性,推导可转为线性求中值(对应的交点最小值)。如下图所示:
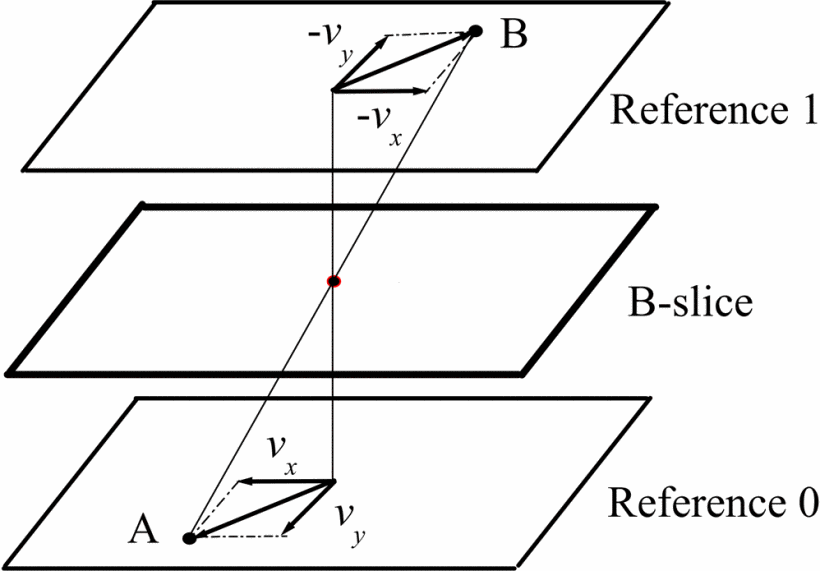
图 3-17 BDOF 构建参考对称光流示意图[29]
假设,当前临近三帧有需要推算分块 m 范围内像素点 p=(x, y) 的灰度。 按时序方向(视屏正常播放方向,图中由下而上) 的前向帧(过去帧)为 R0 有块灰度值 I0 集、当前帧为 Rc 有块灰度值 Ic 集、后向帧(未来帧)为 R1 有块灰度值 I1 集。根据 LK 的局部光流趋同性,分块 m 范围内像素点的光流相等,可记 R0 光流 v⃗A , R1 光流 v⃗B 。
由于人为的有 R0 、 R1 的光流在 Rc 镜像对称,如果记 R0 光流 v⃗A=(Vx, Vy) ,则 R1 光流 v⃗B=(−Vx, −Vy) ,即 v⃗B=−v⃗A 。
那么,将关系代入 LK 条件下的基础光流公式,存在块间光流满足:
{+∇xI0⋅Vx + ∇yI0⋅Vy + ε = −∇tI0−∇xI1⋅Vx − ∇yI1⋅Vy + ε = −∇tI1
因为从 R0→Rc→R1 只 推移单位时间,所以有关时间单位导数近似:
{∇tI0 = I0 − Ic∇tI1 = I1 − Ic⇒∇tI0−∇tI1 = ΔI
则三者间的光流关系可化为:
{I0 − Ic + ∇xI0⋅Vx + ∇yI0⋅Vy + ε = 0I1 − Ic − ∇xI1⋅Vx − ∇yI1⋅Vy + ε = 0
未知量有 Ic 和 (Vx, Vy) 三个,是无法单独依赖上方的方程组,只通过两个约束获取的。 不过,块的光流 仍然 是满足 LK 约束,而 LK 法提供了对光流相对独立的预估,配合背景有:
⎩⎪⎪⎨⎪⎪⎧v⃗A=[+Vx+Vy]=(Mc0T⋅Mc0)−1⋅Mc0T⋅Mt0v⃗B=[−Vx−Vy]=(Mc1T⋅Mc1)−1⋅Mc1T⋅Mt1
即:
[VxVy]=21[(Mc0T⋅Mc0)−1⋅Mc0T⋅Mt0+(Mc1T⋅Mc1)−1⋅Mc1T⋅Mt1]=[2(Mc0T⋅Mc0)−1⋅Mc0T⋅Mt0+2(Mc1T⋅Mc1)−1⋅Mc1T⋅Mt1]
而同理于时域梯度的差值近似。对于分块 m 范围内像素点 p=(x, y) 的空域灰度梯度,也可近似换算为:
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧∇xI0 = 2I0(x+1) − I0(x−1)∇yI0 = 2I0(y+1) − I0(y−1)∇xI1 = 2I1(x+1) − I1(x−1)∇yI1 = 2I1(y+1) − I1(y−1)⇒⎩⎪⎪⎪⎨⎪⎪⎪⎧∇xI0+∇xI1 = Δavg(Ix)=ΔIx¯∇yI0+∇yI1 = Δavg(Iy)=ΔIy¯∇xI0−∇xI1 = avg(ΔIx)=ΔIx¯∇xI0−∇xI1 = avg(ΔIy)=ΔIy¯
代入样本梯度到 Mc=[∑∇xIm, ∑∇yIm] ,Mt=[∑−∇tIm] ,展开可得 (Vx, Vy) 取值:
[VxVy]=⎣⎢⎢⎡∑ΔIx¯2⋅∑ΔIy¯2−∑(ΔIx¯ΔIy¯)⋅∑(ΔIy¯ΔIx¯)∑(ΔIx¯ΔIy¯)⋅∑(ΔIy¯ΔI)−∑(ΔIx¯ΔI)⋅∑ΔIy¯2∑ΔIx¯2⋅∑ΔIy¯2−∑(ΔIx¯ΔIy¯)⋅∑(ΔIy¯ΔIx¯)∑(ΔIx¯ΔIy¯)⋅∑(ΔIx¯ΔI)−∑(ΔIy¯ΔI)⋅∑ΔIx¯2⎦⎥⎥⎤
现在,只有 Ic 是未知的了,而可取范围在分块 m 之内时,对于任意块内点 Ic=Ip 。 代入原方程组即可,有:
Ic Ic =2 I0 + I1 + (∇xI0−∇xI1)⋅Vx + (∇yI0−∇yI1)⋅Vy + ε=2 I0 + I1 + ΔIx¯⋅Vx + ΔIy¯⋅Vy + ε=Ipp(x, y)∈m
式子中的 ε 为误差修正值,一般取 ε=0.5 。
如是,双向光流预测的基本原理,数理推导佐证完毕。
可见,BDOF 的算力消耗重点是在有关 (Vx, Vy) 的求解上。所以,工程化会采用小于当前分块的子块大小做卷积核,使用近似求解快速计算。当然也可以在满足精度要求下,通过模型化解决,思路类似于光流补帧的数据预处理。而由于涉及到规格中的不少工程处理技巧,有关 BDOF 标准化的部分,我们留到 H.266 规格详解时再行展开。
