4.5.1 回归项-平均绝对误差(MAE [Mean Absolute Error])
迭代公式:
图像:
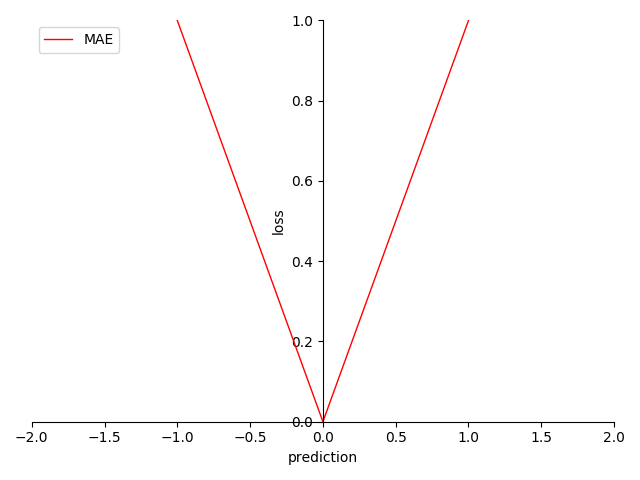
图 4-24 MAE 函数图
特性:
- 契合拉普拉斯分布(Laplace distribution)样本
- 通过样本投影平面的距离向量绝对值,来衡量预测结果
- 导数为常数,梯度迭代线形
- 非光滑(non-smooth)
- 线性处理便于计算
MAE 也被称为 L-1 损失( Loss)。虽然 MAE 常用于机器学习,但它既不是唯一实用的损失函数,也不是适用于所有情形的最佳损失函数。MAE 以样本分布满足拉普拉斯分布的情况为假设,因此对于样本分布满足拉普拉斯分布的样本集,会有更好的效果。MAE 的梯度变换是刚性的,但也因此不容易受到离群值的影响。相应的,MAE 的收敛速度也会更慢一些。
MAE 算子化
利用 C 语言实现对算子的封装,有:
#include <math.h>
#include <stdio.h>
double mae(double *y_true, double *y_pred, int size) {
double sum = 0;
for (int i = 0; i < size; i++) {
sum += fabs(y_true[i] - y_pred[i]);
}
return sum / size;
}
int main() {
int size = 3;
double y_true[] = {0.5, 0.75, 1.0};
double y_pred[] = {0.6, 0.8, 0.9};
double mae_value = mae(y_true, y_pred, size);
printf("The MAE is %f\n", mae_value);
return 0;
}
运行验证可得到结果:
The MAE is 0.100000