4.4.2 Maxout
迭代公式:
图像:
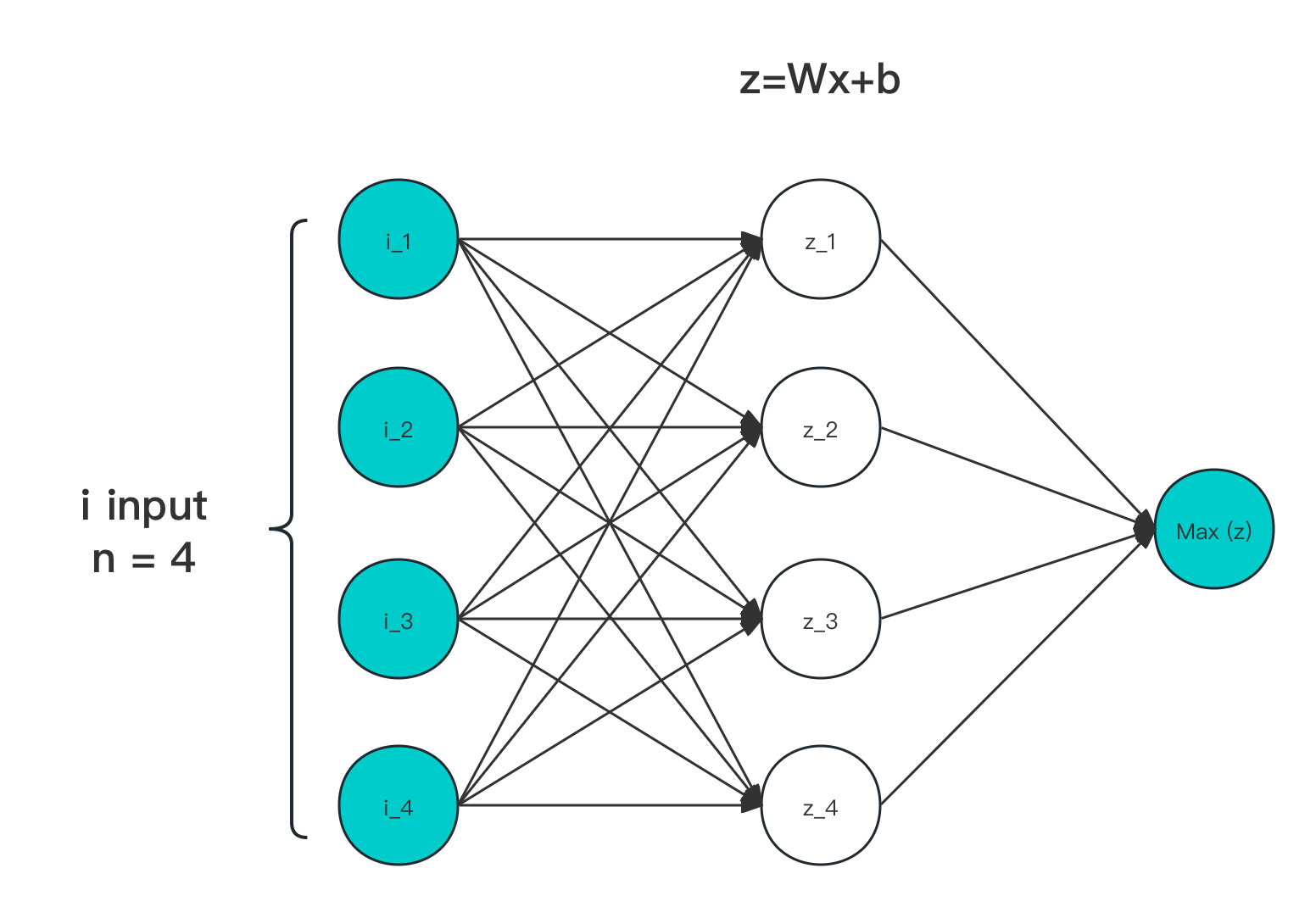
图 4-20 Maxout 输入输出作用示意图
特性:
- Maxout 对输入,走激活层进行线性处理,一个节点即一次线性拟合,参数激增 ≥ k 倍
- 最终是由经由激活层映射后的数据,计算 Max 取极大值
- 本身不面对梯度消失导致和梯度爆炸问题
- 适合配套 Dropout ,作为后级或位于同层一起使用
- 无法用于求导,Maxout 不可微
- 整体处理线性,且非饱和
在 Goodfellow 提出的 Maxout Networks 中指出 Dropout 在层数更多的框架中,能有更好的性能 [13] 。因此,应该有与之匹配的激活函数,来以一种通用的手段将原有模型抽象非线性特征过程,进行层化处理。
Maxout 的设计目的,就是为了更好的使用 Hinton 提出的 Dropout 的性能,提供此类操作。其需要学习的参数就是k个神经元中的权值和偏置,这就相当于常规的激活函数一层,而 Maxout 是两层,而且参数个数增加了 K 倍。
Maxout 能够有效的原理是,任何 ReLU 及其变体等激活函数都可以看成分段的线性函数,而 Maxout 加入的一层神经元正是一个可以学习参数的分段线性函数。所以,理论是可以拟合(无限分割)所有凸函数的。
如下图展示的 k 为 1、2、4 时的情况:
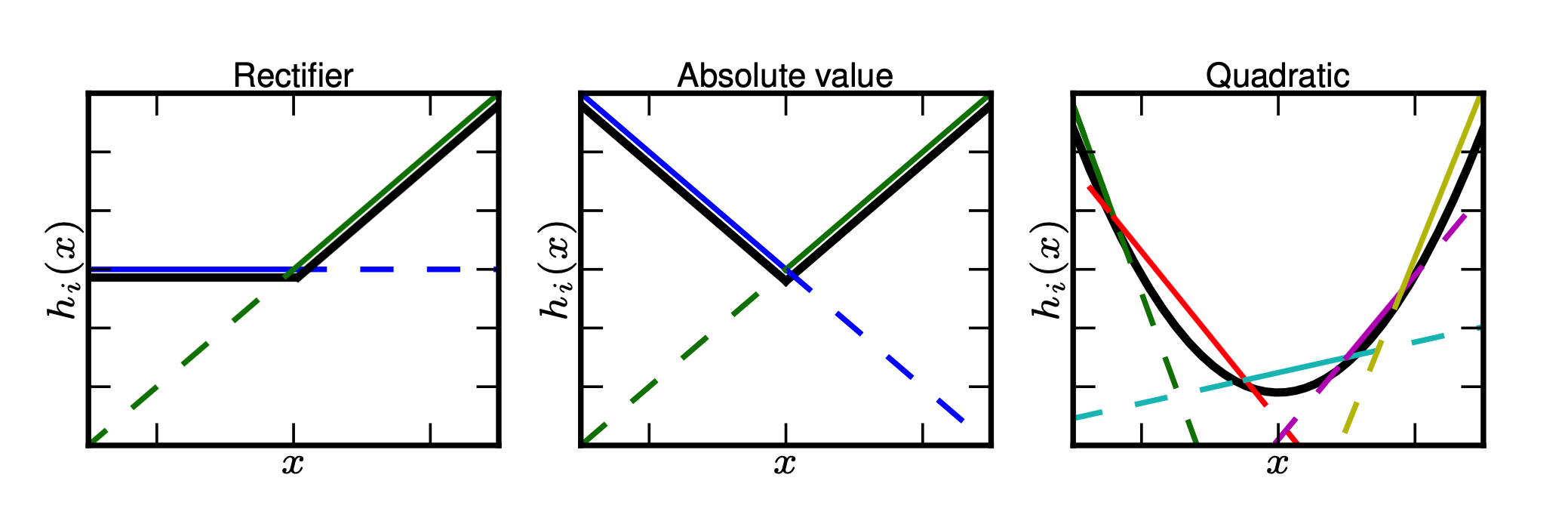
图 4-21 Maxout 凸函数拟合示意图[13]
但是,由于 Maxout 会导致参数激增,从而造成运算量增加,因此不常使用。且由于本身的 不可微 特性,大部分情况下 Maxout 仅能 被用于末尾层中,来对此时已经经过提炼,参数相对较少的特征,进行连接拟合。
Maxout 算子化
利用 C 语言实现对算子的封装,有:
#include <stdio.h>
#include <stdlib.h>
double maxout(double *x, int size) {
double max_value = x[0];
for (int i = 1; i < size; i++) {
if (x[i] > max_value) {
max_value = x[i];
}
}
return max_value;
}
int main() {
int size = 3;
double vecx[] = {0.5, 0.75, 1.0};
double w = maxout(vecx, size);
printf("The maxout of the input vector is %f\n", w);
return 0;
}
运行验证可得到结果:
The maxout of the input vector is 1.000000
和理论表现一致。