4.3.6 Mish
迭代公式:
δ(x)i=x⋅tanh(softplus(x))
即:
δ(x)i=x⋅eln(1+ex)+e−ln(1+ex)eln(1+ex)−e−ln(1+ex)=x⋅(1+ex)2+1(1+ex)2−1=x⋅2+2ex+e2x2ex+e2x=1+2ex+e2x1x
图像:
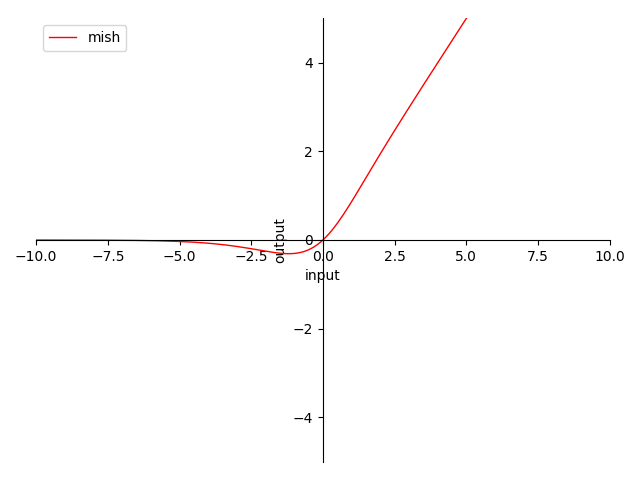
图 4-15 Mish 函数图
特性:
- 0 为中心(zero-centered)
- 输出范围在 [≈0.278, +∞) 之间,导数近似 Switch(x) 但过于复杂
- 输出值域对称,降低在正向堆积风险,但负向变化慢
- 当输入在 (0, +∞) 时,梯度 ≥0.5
- 当输入趋近 +∞ 时,近似于 ReLU,梯度趋近 1
- 当输入趋近 −∞ 时,近似于 ReLU,梯度趋近 0 ,负向过输入大存在梯度消失风险
- Mish 当 β→+∞ 时,趋近 ReLU
- 平滑不单调
Mish 是由 迪甘塔·米斯拉(Diganta Misra) 在 2019 年提出的,其目的是为了在 Swish 基础上,提供一种更有效的激活函数。就目前而言,Mish 的有效性和性价比其实一直处于讨论中 [9] 。
不过,在实验检验下 Mish 并没有那么好用,其各方面特性都与 Swish 高度相似。而且采用 ImageNet 数据集 + MobileNetV2 + FPN 来做物体识别,从结果上反倒没有直接用 ReLU、或者 Swish 效果好,且 MAdds 激增。
因此,本书作者不建议使用。如果既想要利用函数平滑特性来提高优化函数效率,又不想要增加太多算力消耗的话,建议可以考虑 Swish,或 h-Swish(ReLU-N)。
Mish 算子化
利用 C 语言实现对算子的封装,有:
#include <stdio.h>
#include <math.h>
double mish(double x) {
return x * tanh(log(1 + exp(x)));
}
int main() {
double x = 0.5;
double y = mish(x);
printf("The mish of %f is %f\n", x, y);
return 0;
}
运行验证可得到结果:
The mish of 0.500000 is 0.462117
