4.4.1 Dropout
迭代公式:
图像:
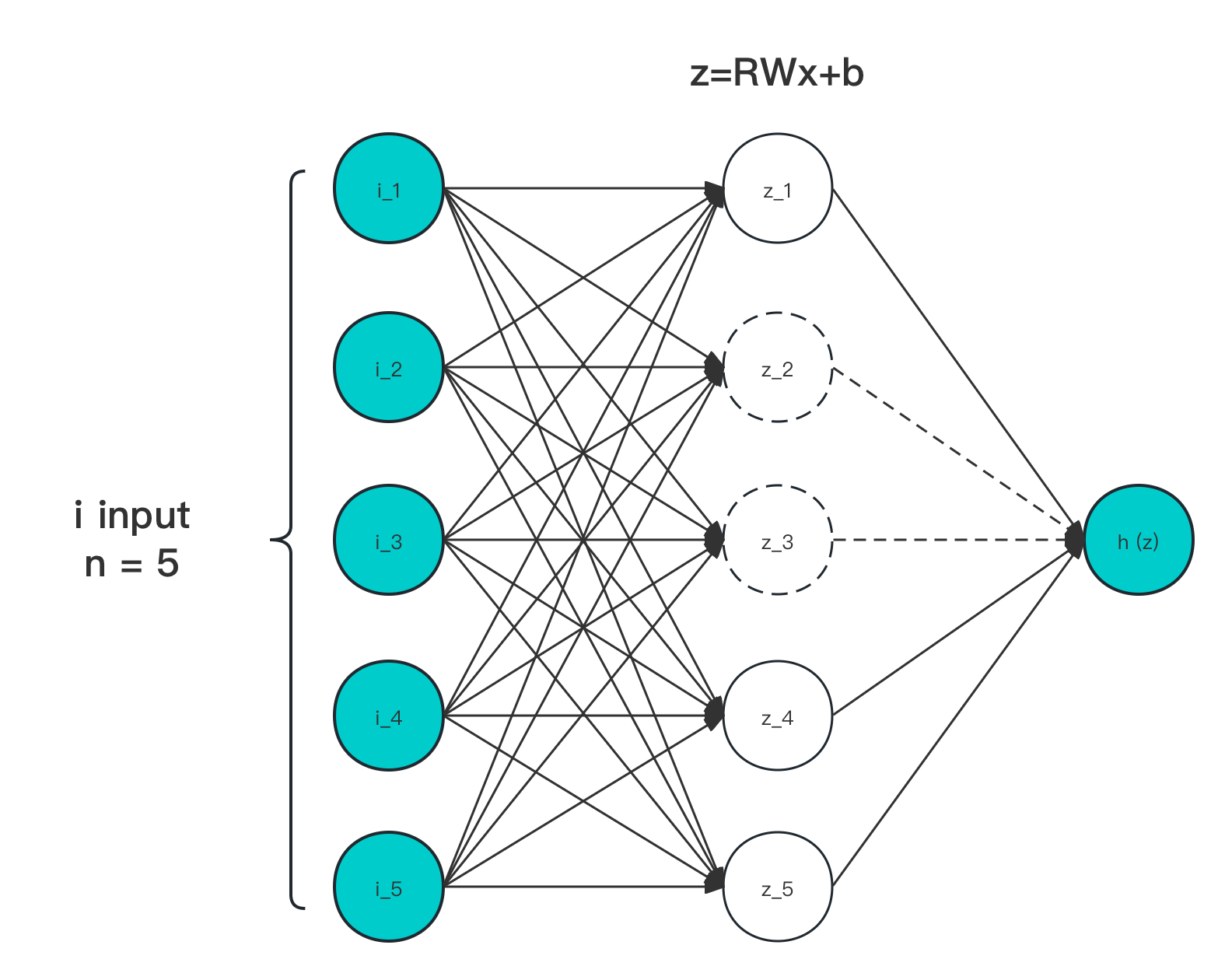
图 4-19 Dropout 输入输出作用示意图
特性:
- Dropout 采用了根据采用者需要的任意设定激活函数,来作为 功效
- Dropout 对每一个激活节点输出 都赋予了根据伯努利分布的随机 或 附加筛选值
- 伯努利分布(Bernoulli Distribution)参数 的值,越大越容易取 ,越小则易取
- 被证明,当 时,能够带来最好的 类正则效果
- 每次触发层计算,伯努利结果 都会根据 重新获取
- 变相取平均,能够减少同层内,神经元间的公适性
- 辅助链接层处理,作用于节点选择,0 丢弃,1 通过
Dropout 是由 Hinton 于 2012 年提出的一种,针对容易过拟合小数据集训练的,过拟合防治手段 [11] 。其本身通过阻塞当前层计算中的生效节点,来实现对当次参与计算权重的随机过滤,从而降低各个训练参数间的关联性。
这个方法随后就被用在了于同年发表的 AlexNet 上,并随着 AlexNet 飞跃式的高准确度(在发表时间点),一起被人们熟知。而随着后续多篇相关 Dropout 数学特征和统计研究的文献中,证明了 Dropout 不止可以被运用于小样本情况,更是相当有效的正则化和模型鲁棒性处理方式。
直到今日,仍然被运用于大量模型的训练中。
Dropout 算子化
利用 C 语言实现对算子的封装,有:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double dropout(double x, double p) {
if (drand48() < p) {
return 0;
} else {
return x;
}
}
int main() {
double x = 0.5;
double p = 0.5;
double y_1 = dropout(x, p);
double y_2 = dropout(x, p);
printf("The dropout of %f with p=%f is %f\n", x, p, y_1);
printf("The dropout of %f with p=%f is %f\n", x, p, y_2);
return 0;
}
运行验证可得到结果:
The dropout of 0.500000 with p=0.500000 is 0.000000
The dropout of 0.500000 with p=0.500000 is 1.000000
和理论表现一致。