2.4.2 色度(Chroma)& 色度平面(Chroma Plane)& 色度图(Chroma Diagram)
色度(Chroma|Chromaticity) 是一个泛指的广义概念,是对除 光亮度(Luminance) 之外,由色调和饱和度或其衍生参数组成的颜色信息的统称。现代工程上的色度概念,最早是在 CIE XYZ 色彩空间对标准色度图的推导过程中引入的。
CIE XYZ 将色度定义为:XYZ 色彩空间内代表颜色的三维向量,由指定平面切割和归一化后,沿 Z 轴垂直方向在 XY 轴平面上二维投影向量。这个用于切割降维和压缩参数范围的平面,被称为 色度平面(Chroma Plane|Chromaticity Plane)。整个色彩空间色域在 XY 轴平面的二维投影,被称为 CIE xyY 色度图(CIE xyY Chromaticity Diagram),简称 色度图(Chroma Diagram)。
为什么是 xyY 色度图?因为决定颜色的除了 xy 代表色度外,还需要光亮度(Luminance)关键量。CIE XYZ 直接取用颜色在 XYZ 色彩空间里的 Y 方向分量,代替指代光亮度。
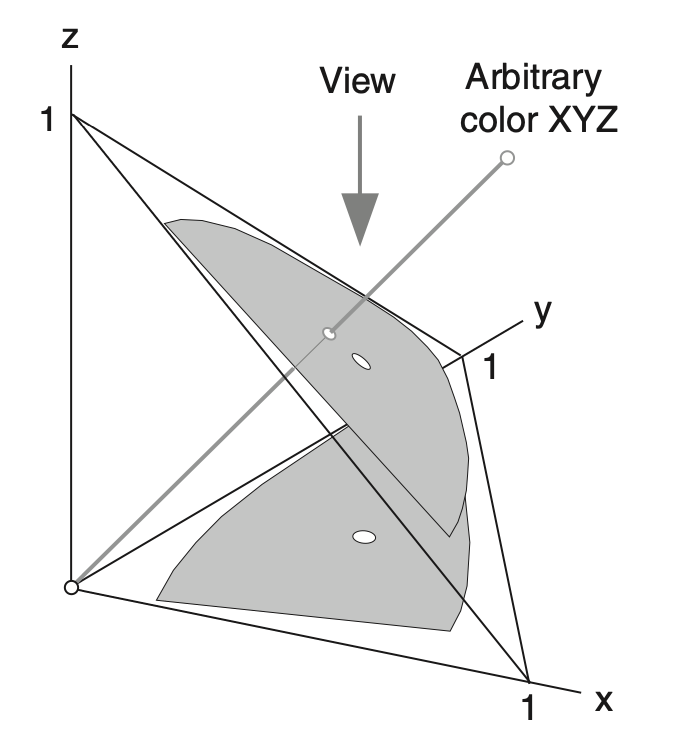
图 2-13 CIE 色度平面切割标准色域并投影色度图的示意图
可见,使用色度的色彩空间,色度的量化和其内部参数的选取息息相关。不同的色彩空间在色度的定义上,存在着表述上的不同。在大多数情况下,CIE XYZ 之后的色彩空间,都会取用 CIE 测定的 700nm 波长标准红点(Red Point) 为 基准轴正轴方向,来构建自身的色度参数。究其原因是,相同的基准可以便于将自身色域转换到 CIE XYZ 统一度量衡上对比。所以,色度也常常被直接用 CIE XYZ 色彩空间的定义来表示。
CIE XYZ 色彩空间取用 [X=1, Y=1, Z=1] 构成的三棱锥底面所在平面为色度平面。该平面上的 XYZ 坐标系内点存在关系:
记 XYZ 色彩空间中存在颜色 在 XY 平面的投影为 ,则有:
在已知 的情况下,也可以反向获得 :
所以,只要根据 值,就能将色度图上的颜色还原到 XYZ 实际坐标。而其中的 值,就是 CIE 中颜色色度的表示形式。
那么在颜色能够被统一描述的前提下,颜色间的差异怎么来说明呢?