4.5.5 分类项-对数损失(Log Loss)
迭代公式:
图像:
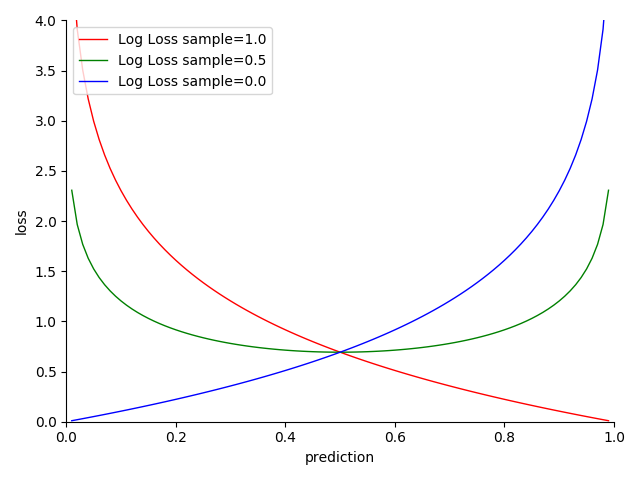
图 4-29 Log Loss 函数图
特性:
- 契合逻辑分布(Logistic distribution)样本,拟合 Sigmoid 模型
- 二分类下的交叉熵损失表现,二者本质等价
- 越接近目标,损失越小
- 越趋近两极,结果越准确
- 基于贝叶斯统计(Bayesian statistics),采用交叉熵估计
- 光滑(smooth),适合优化算法
- 对数计算,算力消耗相对较高
对数损失(Log Loss) 是一种利用最小化负对数似然,即交叉熵最小化,来进行逻辑回归的损失函数。实际上,Log Loss 相当于 只包含两种分类 情况下的交叉熵损失函数。其所适应逻辑分布样本集,我们认为只存在 “是/否”两种情况 的 独热向量(one-hot vector) 集合。对于此类样本集,我们一般采用 Sigmoid 将输出压缩到 范围内,以便于输出百分比估计结果,作为预测结果的置信水平。而从 Log Loss,我们不难看出,最小化交叉熵函数本质就是对数似然函数的最大化。
注意,对数损失只能用来区分 “是/否” 为某个物体。
这一点在初学者首次接触时,容易与交叉熵损失搞混,从而选错分类项(比如目标是多分类检测)需要小心。
Log Loss 算子化
利用 C 语言实现对算子的封装,有:
#include <math.h>
#include <stdio.h>
double log_loss(double *y_true, double *y_pred, int size) {
double sum =0;
for (int i =0; i < size; i++) {
sum += y_true[i] * log(y_pred[i]) + (1 - y_true[i]) * log(1 - y_pred[i]);
}
return -sum / size;
}
int main() {
int size = 3;
double y_true[] = {0.5, 0.75, 1.0};
double y_pred[] = {0.6, 0.8, 0.9};
double log_loss_value = log_loss(y_true, y_pred, size);
printf("The log loss is %f, for object class 'apple'", log_loss_value);
return 0;
}
运行验证可得到结果:
The log loss is -0.056644, for object class 'apple'