2.3.4 经典三刺激函数(Tristimulus Values Functions)
CIE 在 1931 年同年提出 CIE XYZ 色彩空间,尝试通过人为设计的色感函数 [12] [13],来避 RGB 的 负色匹配 问题。为了区别于 CIE RGB 中,通过实验测定拟合而得的三原色色感函数。我们将新的函数称为 CIE 三刺激函数(Tristimulus Values Functions),用来代替原有 r(λ) 、 g(λ) 、 b(λ) ,记为 x(λ) 、 y(λ) 、 z(λ) 。三个刺激函数对应的刺激曲线如下图:
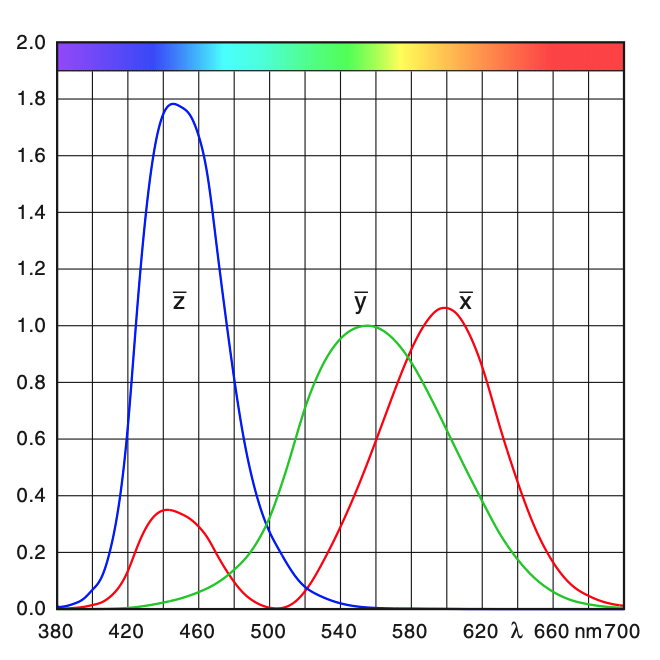
图 2-10 CIE 1931 XYZ 采用的三原色色感函数
CIE 在三个刺激函数为基准下,确定了的不同波长光的三刺激值分离函数:
X=∫0∞S(λ)x(λ)dλY=∫0∞S(λ)y(λ)dλZ=∫0∞S(λ)z(λ)dλ
其中,
有 r(λ) 、 g(λ) 、 b(λ) 是将理想刺激值峰值 (μ,σ1,σ2) ,带入高斯公式所得,这和 RGB 色感函数的拟合有一定的不同。峰值 (μ,σ1,σ2) 中, μ 代表峰值波长, σ1 代表 μ 值左侧生效范围偏移量, σ2 代表 μ 值右侧生效范围偏移量。XYZ 在度量峰值上取用了理想状态值,有:
g(λ; μ,σ1,σ2)={exp(−21(λ−μ)2/σ12),exp(−21(λ−μ)2/σ22),λ<μ,λ≥μ.
推导而出:
x(λ)=1.056g(λ; 599.8, 37.9, 31.0)+0.362g(λ; 442.0, 16.0, 26.7)−0.065g(λ; 501.1, 20.4, 26.2)y(λ)=0.821g(λ; 568.8, 46.9, 40.5)+0.286g(λ; 530.9, 16.3, 31.1)z(λ)=1.217g(λ; 437.0, 11.8, 36.0)+0.681g(λ; 459.0, 26.0, 13.8)
而 S(λ) 仍然为为目标波长 λ 的光谱功率分布函数:
S(λ)=Le(λ)θ=2∘≈dAdΩd2Φe(λ)=dΩdEe(λ)
同样的,指定波长 λ 的光线,就能被相对化表示为:
Ray(λ)=C(X,Y,Z)
通过以 (X,Y,Z) 代替 (R,G,B) 的度量方式,CIE XYZ 解决了负色匹配问题。为了区别于 (R,G,B) 光学三原色的称谓,我们将 (X,Y,Z) 称为 三刺激值(Tristimulus Values)。
不过,CIE 1931 RGB & CIE 1931 XYZ 中对于光学三原色标准波长的测量/设置,在现代光学体系中被认为有所偏颇的。在选取基准波长时,1931 RGB 蓝绿取用气态水银(Hg)放电获谱线产生的峰值波长 435.8nm(蓝)和 546.1nm(绿),而红色却因为人眼在对 700nm 波长附近的颜色感知几乎无变化的情况下,人为介入设定为还原配色实验理想值 700nm。这一历史局限性导致的情况,也被基于 RGB 测定而考量的 XYZ 继承了。以致于为两者的 “均色问题” 埋下了伏笔。
即便如此,经典三原色函数和三刺激函数,仍然为现代色彩体系奠定了基础公式。使我们能够 以数理形式转换对应目标波长的目标光波,到相应的度量衡系统。
