4.3.7 Swish
在本节开始时,我们曾提到过可以用 Swish 来代替 Sigmoid 在模型中的作用,以获取平滑非线性特征。那么 Swish 具体是什么样的呢?
Swish & Swish-β
迭代公式:
迭代公式(参与训练动态参数版本,Swish-β ):
图像:
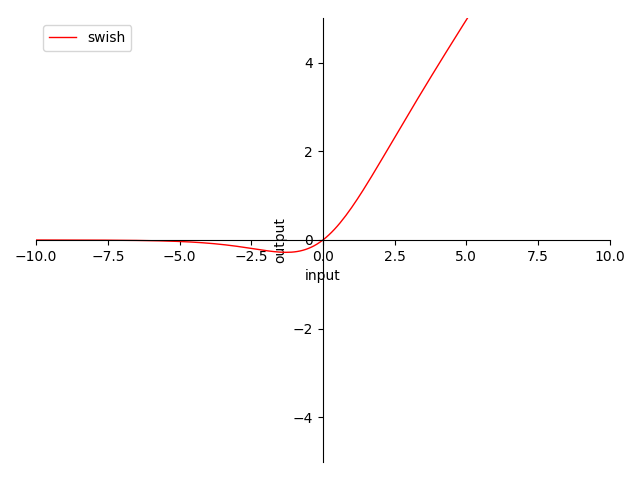
图 4-16 Swish 函数图
特性:
- 0 为中心(zero-centered)
- 输出范围在 之间,导数为
- 输出值域对称,降低在正向堆积风险,但负向变化慢
- 当输入在 时,梯度
- 当输入趋近 时,近似于 ReLU,梯度趋近
- 当输入趋近 时,近似于 ReLU,梯度趋近 ,负向过输入大存在梯度消失风险
- Swish-β 当 时,趋近 ReLU
- 平滑不单调
Swish 是由谷歌实验室在 2017 年提出的,提出以后其实一直争议不断。Swish 被谷歌认为是一种可以完美替代 ReLU 的简单激活函数,在论文中的演示里,其使用同模型在 Mobile NASNet-A (Zoph et al., 2017) 和 Inception-ResNet-v2 (Szegedy et al., 2017) 数据集上分别带来了0.9% 和 0.6% 的准确度提升 [10] 。不过业界普遍认为这个是因为数据集完善带来的。
Swish 作为一种平滑函数,它的特性和 SoftPlus 类似,优势都体现在优化函数的连续处理上。另外不单调,也能够提供更灵活的特性变化。兼容算力消耗,Swish-β 也不失为一种良好的选择。否则还是建议使用 ReLU 处理。
h-Swish
迭代公式:
图像:
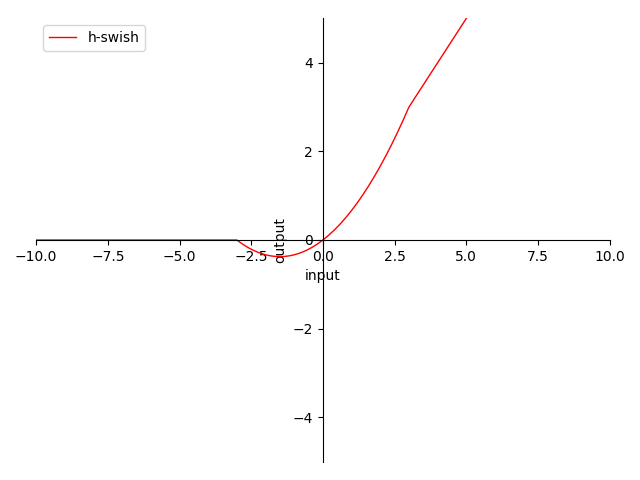
图 4-17 h-Swish 函数图
特性:
- 非 0 为中心(non-zero-centered)
- 输出范围在 之间
- 输出 ,反向传播(BP)权值正向堆积(梯度始终 )
- 当输入在 时 梯度为 ,完美解决梯度消失问题 及 梯度爆炸问题,等效 ReLU
- 当输入在 时 梯度为 ,面临神经元死亡问题,等效ReLU
- 当输入在 时 梯度为 , , ,梯度
- 非指数处理便于计算
- 非平滑不单调
h-Swish 是由谷歌实验室在 2019 年的 MobileNetV3 中提出的,用于作为两种 MobileNet 关键优化手段中的一种 [11] 。h 表示 hard。h-Swish 与 Swish 最大的不同就在于,用近似 sigmoid 的 ReLU-6(x+3) / 6 代替了 Sigmoid,也被称为 h-Sigmoid。
h-Swish 保留了 Swish不单调的特性,能够更好的进行非线性特性的引入。但是 h-Swish 也保留了 Swish 的有效范围特性。且因为采用 h-Sigmoid 处理,在样本输入小于 -3,将会导致神经元死亡问题。但是 h-Swish 的优势也同样明显,因为单激活函数最高只用到二次幂,实际运算当中较 Swish 节约了相当的算力。因此,建议根据情况,选择特征缩放处理(或单边限定偏移)后使用。其本身还是很有潜力的新兴激活函数。
需要注意的是,考虑到计算便利性和 Tanh 与 Sigmoid 的函数趋势近似。在工程中,我们 采用 Tanh 代替原论文的 Sigmoid 进行 Swish 族的算子化。同理也适用于,采用 log 代替 h-Sigmoid。从而简化了计算过程。
Swish 族算子化
利用 C 语言实现对算子的封装,有:
#include <stdio.h>
#include <math.h>
double swish(double x) {
return x * tanh(x);
}
double swish_beta(double x, double beta) {
return x * tanh(beta * x);
}
double h_swish(double x) {
return x * tanh(log(1 + exp(x)));
}
int main() {
// Swish
{
double x = 0.5;
double y = swish(x);
printf("The swish of %f is %f\n", x, y);
}
// Swish-β
{
double x = 0.5;
double beta = 1.0;
double y = swish_beta(x, beta);
printf("The swish-beta of %f with beta=%f is %f\n", x, beta, y);
}
// h-Swish
{
double x = 0.5;
double y = h_swish(x);
printf("The h-swish of %f is %f\n", x, y);
}
return 0;
}
运行验证可得到结果:
The swish of 0.500000 is 0.462117
The swish-beta of 0.500000 with beta=1.000000 is 0.462117
The h-swish of 0.500000 is 0.462117
至此,常用激活函数基本梳理完毕。
其实,常用于中间层的激活函数,往往都是简单激活函数,这样能够在引入非线性特征的同时,相对较小或者几乎不怎么消耗算力资源。而在最终阶段,常常使用复杂的激活函数来做分类器,或结果控制的操作。相对来说,复杂激活函数的使用往往都放在最终阶段的原因,就是因为其过于复杂的特性,能够适应更严格的情况,但也相对更耗费算力资源,无法频繁使用。
至于如何更好的使用激活函数,建议结合激活函数的特性,将输入值进行适当的放缩,例如:如果使用Sigmoid,那么我们可以先行放缩上层输入到 ( -5, 5 ) 的范围内,这样一定程度的避免梯度消失问题。所以,如何根据选用的激活函数,适当的调整上层输入,将会对结果大有裨益。
另外,个人理解 光滑(smooth) 函数类型的激活函数,其优势在于 能够更好的配合优化方法,而且能够 解离 不同分类之间的差异性(连续非离散,差异细化),使得模型具有更好的鲁棒性。但是因为算力上不占优势,建议用在 last stage 部分。 除此之外,非单调性也是近期激活函数新的关注点,业界的研究显示,适当的引入非单调性,能够很好的增强激活函数将源数据,输出为非线性数据的信息保存水平。
综合而言,建议现阶段使用激活函数,优先考虑:ReLU、LReLU、ReLU-N、h-Swish,根据是否需要配合优化算法(利用 smooth 特性),进一步选择是否采用:Softplus、Swish。结合现有硬件水平,适度的考虑含有指数计算的激活函数。