4.3.5 ELU & SELU
迭代公式:
图像:
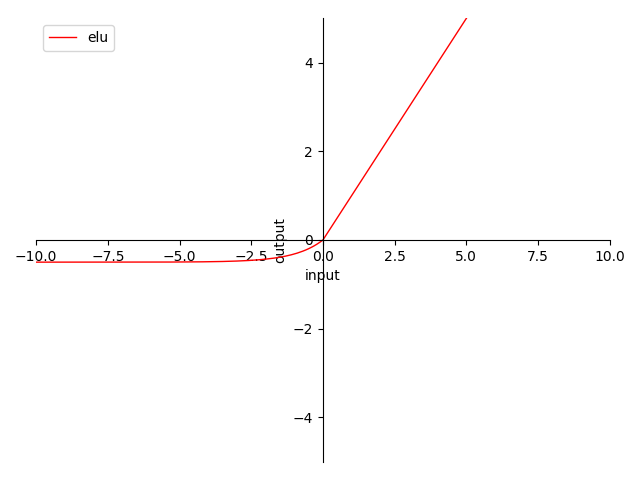
图 4-14 ELU & SELU 函数图
特性:
- 0 为中心(zero-centered)
- 输出范围在 之间,称 为常量乘数
- 输出值域对称,降低在正向堆积风险
- 当输入在 时,梯度为常量 ,完美解决梯度消失问题 及 梯度爆炸问题
- 当输入在 时,梯度以 形式变化,仍然存在梯度消失风险
- 公式中的 可取经验值,也可参与迭代
- 指数计算,较为消耗资源
ELU(2016)被称为 指数线性单元。也是一种为了处理 ReLU 梯度消失问题而提出的激活函数。 ELU 比之 ReLU 其他几种变体,最大的特点就是曲线平滑。而 SELU 则是在原有 ELU 激活函数的基础上,再乘以一个系数(通常取固定常量),即 。根据原作者 京特·克兰鲍尔(Günter Klambauer) 在论文《Self-Normalizing Neural Networks》中的描述 [8] ,推荐取 的经验值。
SELU 可使输入经过一定层数处理后,变为固定分布。
ELU & SELU 算子化
利用 C 语言实现对算子的封装,有:
#include <stdio.h>
#include <math.h>
double elu(double x, double alpha) {
return x >= 0 ? x : alpha * (exp(x) - 1);
}
double selu(double x, double alpha, double lambda) {
return lambda * (x >= 0 ? x : alpha * (exp(x) - 1));
}
int main() {
// ELU
{
double x = -0.5;
double alpha = 1.0;
double y = elu(x, alpha);
printf("The ELU of %f with alpha=%f is %f\n", x, alpha, y);
}
// SELU
{
double x = -0.5;
double alpha = 1.6732632423543772848170429916717;
double lambda = 1.0507009873554804934193349650124;
double y = selu(x, alpha, lambda);
printf("The SELU of %f with alpha=%f and lambda=%f is %f\n", x, alpha,
lambda, y);
}
return 0;
}
运行验证可得到结果:
The ELU of -0.500000 with alpha=1.000000 is -0.393469
The SELU of -0.500000 with alpha=1.673263 and lambda=1.050701 is -0.428348