4.3.1 Sigmoid
迭代公式:
图像:
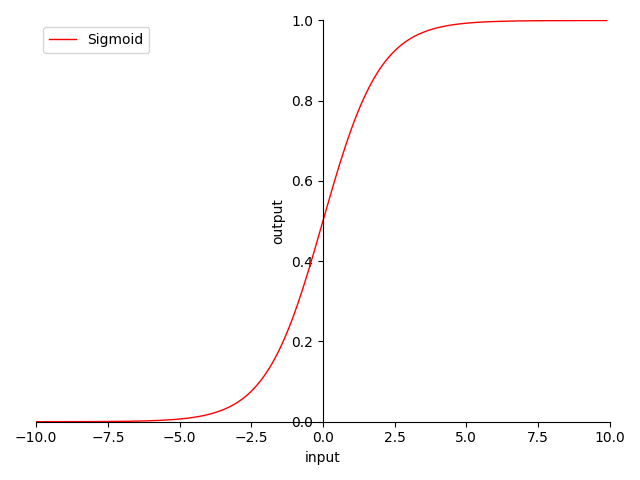
图 4-9 Sigmoid 函数图
特性:
- 非 0 为中心(non-zero-centered)
- 输出范围在 之间,导数
- 输出 ,反向传播(BP)权值正向堆积(梯度始终 )
- 输入 或 时,输出近乎无变化,逐层梯度趋 ,更易导致梯度消失
- 指数计算,较为消耗资源
Sigmoid 激活函数梯度趋近于 0,即软饱和。这会导致BP在该区域部分的导数,无法有效的传递误差至上层(趋 0 失效),导致前层权值无更新,从而无法收敛。且因为 非 0 为中心,使得我们在使用它做激活函数时,需要考虑数据对称(zero-mean data)。
Sigmoid 也可以根据情况,使用其他算法代替,例如(swish、h-swish)。通常在二分问题上采用 Sigmoid 是不错的选择,诸如:是否是某一类、问题对错,即古典逻辑回归(Classical Logical Regression)。
Sigmoid 算子化
利用 C 语言实现对算子的封装,有:
#include <stdio.h>
#include <math.h>
double sigmoid(double x) {
return 1 / (1 + exp(-x));
}
int main() {
double x = 0.5;
double y = sigmoid(x);
printf("The sigmoid of %f is %f\n", x, y);
return 0;
}
运行验证可得到结果:
The sigmoid of 0.500000 is 0.622459