1.4.1 乐理:音调(Notes)& 五度圈(Circle of Fifths)
在声音三要素开始的部分,我们已经简单介绍了一些乐理基础概念。而乐理对声音的描述,都是基于 音调(Note) 为出发点的。通过音调指向基音,建立主观参考系下的客观不变量,从而构造统一的联系。结合 系统的 记录方式,完成对一定时间段下,音乐的保存。
所以,乐谱(Musical Notation) 就是一种,以手动编排抄录的方式,进行声音持续化存储的早期人工手段。而 乐理音调(Music Note),以下我们简称为 音调(Note),就是一种粗粒度(相对于数字时代编码调制而言)的固定采样。
依旧采用 八度音(Octave)的音阶体系,首先需要建立乐理(艺术)心理(感观)转换。
音调(Notes)的 音程尺度描述(ISN [Interval Scale Name])
这个我们已经介绍过。 八度音阶(Octave) 以钢琴音级为 4 时为准,包括音名、半音在内,共有 12 个,即 C、C♯/D♭、D、D♯/E♭、E、F、F♯/G♭、G、G♯/A♭、A、A♯/B♭、B 。为方便说明,我们补充下一级的 C5 到表中,有:
| C | C♯ D♭ |
D | D♯ E♭ |
E | F | F♯ G♭ |
G | G♯ A♭ |
A | A♯ B♭ |
B | C5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 261.63 (0) |
277.18 (+1) |
293.66 (+2) |
311.13 (+3) |
329.63 (+4) |
349.23 (+5) |
369.99 (+6) |
392.00 (+7) |
415.30 (+8) |
440.00 (+9) |
466.16 (+10) |
493.88 (+11) |
523.25 (+12) |
明明是 八度音,却有包扩 C5 在内的 13 个音调。尺度不一太尴尬了,怎么办呢?
音乐艺术先贤们也遇到了同样的问题。于是,根据 两两相邻音调间的音程(Interval),在同音级下,有了不同的 音程尺度描述(ISN [Interval Scale Name])。正好作为转换起点。
在 C4 所在第 4 音级取 ISN。所有音调与 C4 相比音程为:
| Notes | Frequency(Sequence) | Interval Scale Name | Interval as Notes |
|---|---|---|---|
| C4 | 261.63 (0) | 纯一度(P1 [Perfect Unison]) | 0 |
| C♯/D♭ | 277.18 (+1) | 小二度(m2 [Minor Second]) | 0.5 |
| D | 293.66 (+2) | 大二度(M2 [Major Second]) | 1 |
| D♯/E♭ | 311.13 (+3) | 小三度(m3 [Minor Third]) | 1.5 |
| E | 329.63 (+4) | 大三度(M3 [Major Third]) | 2 |
| F | 349.23 (+5) | 纯四度(P4 [Perfect Fourth]) | 2.5 |
| F♯/G♭ | 369.99 (+6) | 增四度(A4)/减五度(d5) | 3 |
| G | 392.00 (+7) | 纯五度(P5 [Perfect Fifth]) | 3.5 |
| G♯/A♭ | 415.30 (+8) | 小六度(m6 [Minor Sixth]) | 4 |
| A | 440.00 (+9) | 大六度(M6 [Major Sixth]) | 4.5 |
| A♯/B♭ | 466.16 (+10) | 小七度(m7 [Minor Seventh]) | 5 |
| B | 493.88 (+11) | 大七度(M7 [Major Seventh]) | 5.5 |
| C5 | 523.25 (+12) | 纯八度(P8 [Perfect Octave]) | 6 |
表内抽象的音程名中,出现了一些 非精确量词(Inaccurate Quantifiers) 被使用其中。确切的来说,基础量词有五种,由小到大分别是(注意简写时的 大小写区分 ):
小(m [Minor])、纯(P [Perfect])、大(M [Major])
增(A [Augmented])
上述量词怎么来的呢?直接意义上,这是两套体系。一套基于 相对音程,一套基于 绝对音程。简单来说,取整数 表示通用数字级。则
绝对音程(n.AI [Absolute Interval]),采用 减(d [Diminished]) 、 增(A [Augmented]),是取用第 4 级的纯一度(P1)就是 C4 261.63 Hz 作为原点。记原点音调音序为 ,目标音调音序为 ,有:
- 减 k 度(dk [Diminished k]),意味着 ;
- 增 k 度(Ak [Augmented k]),意味着 ;
相对音程(n.RI [Relative Interval]),采用 小(m [Minor]) 、 纯(P [Perfect]) 、 大(M [Major]),是一种差值概念。记被比较的音调音序为 ,而目标音调音序为 ,有:
- 小 k 度(mk [Minor k]),指 时对应 ;
- 纯 k 度(Pk [Perfect k]),指 时对应 ;
- 大 k 度(Mk [Major k]),指 时对应 ;
而在 所有音调与 C4 相比的音程表 中,之所以出现了 F♯/G♭ 用绝对音程(Absolute Interval)与 A440 440 Hz 相比,其它采用相对音程(Relative Interval)与 C4 261.63 Hz 相比的原因,正是在 时,用相对音程的 小(m)、纯(P)、大(M) 无法描述 该音程。所以,不得已 才借用了绝对音程的 增(A)、减(d) 描述法。
现在,我们已知同音级下的音程表示了。不过实际使用中,往往会出现两个参与计算的音调是跨级的情况。虽然两方法都适用于跨越多音级(跨级)的音程计算,但 绝对音程(n.AI)和 相对音程(n.RI)在对此的表达上,还是存在较大差异的。
绝对音程(n.AI)的 跨级计算
绝对音程(n.AI) 因为存在原点而且不区分范围,因此可以在单一方向上持续增,或持续减。不过因为往低频方向持续运动,会可能有负值。
所以,除 情况外,我们一般只用它来像高频方向计数。而这种处理使得以 n.AI 公式计算出来是多少 k ,就应该称为增减多少 k 度(AK/dK)。
例如,
- 从 D4->C6 的音序差 ,为 减十三度(d13) ;
- 从 D4->F6 的音序差 ,为 增十四度(A14) ;
- 从 C4->F6♯/G6♭ 的音序差 ,为 减十七度(d17) ;
相对音程(n.RI)的 跨级计算
相对音程(n.RI) 的跨级计算就要麻烦一些。这个麻烦主要体现在相对音程的音程尺度描述(ISN)在带上 从绝对音程中借用的 增四度(A4)/减五度(d5)后,也仅有 13 个。
所以,在跨级描述上,相对音程情况需要引入其它的量词用以记录级数差。一个简单的方法就是 在公式基础上,根据跨越的级数,在称为中增加 级数 x 七度 的大小。
例如,
- 从 D4->C6 的音序差 ,为 小十四度(m14) ;
- 从 D4->F6 的音序差 ,为 小十七度(m17) ;
但当 时, 借用 的 增四度(A4)/减五度(d5) 又不能 换回绝对音程来重新计算,该怎么办呢?
相对音程针对这种情况,引入了 倍数(Multiples)来辅助标记。即 m倍增/m倍减。
例如,
- 从 C4->F6♯/G6♭的音序差 ,有 的值,称为 二倍增四度(AAA4)/二倍减五度(ddd5)。即多出来的倍数 ,就代表着需要 多写 几个 增(A)或 减(d)。
至此,结合 时的倍数描述 和 “±7” 度法,我们就能够从乐理(艺术)上形容跨多音级(Steps)的相对音程了。
不过,这样的算法要求我们知道当前音调的音序。但因为一般情况下,乐谱中采用的都是确认 大/小调 主音(Keytone) 后,对包含音调距离主音音程的符号化记录。所以, 必须要能获取主音的音序才能相对计算出,乐谱中的实际乐符的音程,进而推得音序和标的频率。
大/小调(Major Scale/Minor Scale)
什么是大/小调?大/小调(Major Scale/Minor Scale) 是古典音乐中,对一组参与演奏音调韵律的总结。不同 大/小调所采用的音调是不同的。 这里有相当多的乐理(艺术)细分,为了便于说明,除非特别声明,否则都认为 未指明类型的 大/小调 皆属于 自然音阶(Diatonic Scale)。
其中 大/小调 中的 大/小,虽同名于 相对音程 的 大/小,但两者却 并不是一个概念。大/小调 对大/小 的定义,并不是指音程差,而是指组成 大/小调 的自然音阶(Diatonic Scale)中 包含的一系列古典音调(Classical Tone)。
例如,C 大调(Major C)的主音(Keytone)就是 C4 261.63 Hz 。但总共包含:
所以,如果直接算。 从乐谱到我们可以使用的音程尺度名称间,还需要进行一次大/小调到实际音调组间的转换。
之后,才能够利用相对音程公式,完成快速反向计算来得到换算音序值。再用得到的音序值,查询基音频率。
因此,必须要依赖于 快速确定 大/小调 的手段。该手段就是 五度圈查询法。
五度圈(Circle of Fifths)查寻法
回到音乐(艺术)史早期,人们制定了诸如:古典五律、十二平均律等非精确度量衡。而在 十二平均律(12-TET [12-Tone Equal Temperament]) 中,将属于自然音阶(Diatonic Scale)的自然大调(Major Scale)第 4 音级 C–D–E–F–G–A–B 取为标准(此处取现代声学标准,明朝皇族世子朱载堉发明时,近代物理才刚起步,还未有机械波概念,所以仍是依赖于古筝琴律),而对 C-B(12-TET 采用的实际是 等效到同间隔的 C-F ) 间音调进行了 比例分割。
此举启发了人们对古典五律的划分,从而有了 自然大调(Major Scale),即 C大调, 的五度圈(Circle of Fifths)查寻法。这是一种将上文 12 音调以圆圈的形式串联的表示方式。当然,人们创造出该方法的时候,是凭借着历史经验总结而来的。不得令人感叹其中的智慧。
有速查图如下:
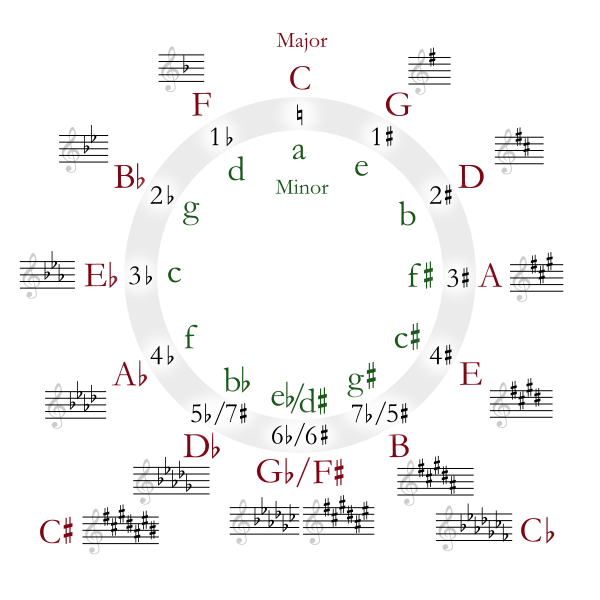
图 1-11 五度圈音调表示意图 [9]
此即为最早且被应用至今(如吉他等)的快速跨级查表法。
图中,大写字母代表自然大调(Major), 小写字母代表自然小调(Minor)。 音调(Note)所带的升降号( ),在音乐(艺术)中,被称作 调号(Key Signatures)。
以此为出发点,转换到同音级处理。就有, 同圈层 的音调,相邻两个音调间的音程(Interval),顺时针时差值为 纯五度(P5),逆时针时为 纯四度(P4)。称为 相邻调(Adjacent Key)。
五度圈中位于 同位置内外圈 的大小调,两者间的 主音(Keytone) 音程为 小三度(m3),且 主音调号(Key Signatures)相同。称为关系调(Relative Key)。
当我们从内圈向外查找,有音程:
- a->C(如 A4->C5)有 ,为 小三度(m3) ;
- d->C(如 D4->C5)有 ,为 小七度(m7) ;
- d->E(如 D4->E5)有 ,为 大九度(M9) ;
所以, 以升/降序来看,五度圈是螺旋上升/下降的。
我们以表中 代表着进入了 更上层高音级,而 代表降至 更下层低音级。则跨越三层的升序大调五度圈,就如下所示:
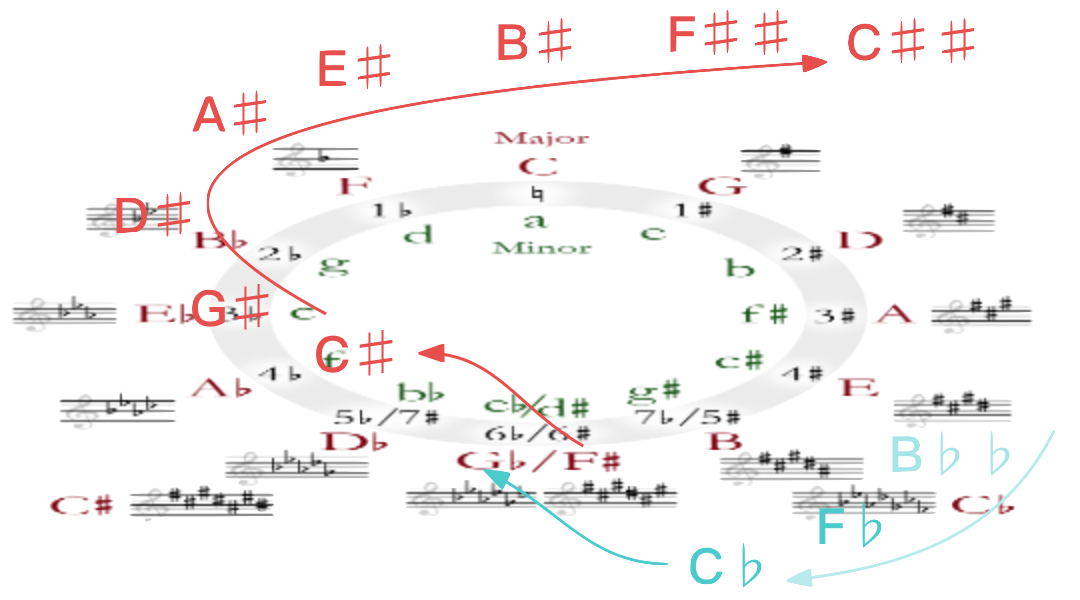
图 1-12 三层五度圈(升调方向)音调表示意图
自然大/小调,均包含 7 个音调。分别是主音前 1 个音调,和包括主音在内的后 6 个音调。在此基础上,结合五度圈的维度特点,只需要以 滑动窗口来标记对应调位,即可速查大小调中的各个音调:
例如,
- 查表得 大调的基础音调,组成为
- 查表得 大调的基础音调,组成为
- 查表得 大调的基础音调,组成为
- 查表得 大调的基础音调,组成为
五度图中一圈(不升降),就是音级为 4 时 ISO 16 标准的 A440 八度音阶 C4 子表。
| C | C♯ D♭ |
D | D♯ E♭ |
E | F | F♯ G♭ |
G | G♯ A♭ |
A | A♯ B♭ |
B | C5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 261.63 (0) |
277.18 (+1) |
293.66 (+2) |
311.13 (+3) |
329.63 (+4) |
349.23 (+5) |
369.99 (+6) |
392.00 (+7) |
415.30 (+8) |
440.00 (+9) |
466.16 (+10) |
493.88 (+11) |
523.25 (+12) |
而当发生升降时,对于在表中没有对应的额外 个 标志,提升或降低 个音级再次查对应 音级,对应的 音阶频率子表。
例如,
- 对于五度圈更上一层的 ,而 。
至此达成,利用音调在乐理上的音程尺度描述(ISN),以两种参考系的关联,利用公式或搜图,来转换到工程音序频率关系了。从而方便我们根据 乐理音调(Musical Note)查询它的 基波(Fundamental)频率。
ISN 本身在乐理(艺术)上,是人为认为的尺度平均的。不过,乐理上的平均,是否意味着实际频率的平均呢?结合 A440 频率音序公式(FSF)判断可知, 乐理平均并不意味着均匀的频率划分。这和人耳的听感息息相关。
经过近代心理声学对人耳感观的样本统计测定后,了解到其中的一些端倪。
音调(Notes)的 频率比(Frequency Ratio)
我们发现,以 C4 261.63 Hz 为标准,人对与 C4 频率呈现一定特殊比例的音调,会有更好的听感反馈(详见 等响曲线)。而以某些相应比例,按照从低到高的非线性变化,会使人产生 聆听时的平滑感(Smoothly)。根据这样的研究结果,可见古人间接以 非线性频率比 (虽然发明命名法的时候并无测定,而是后续心理声学补测), 主观确定了音调划分。
仍然采用该音级 4 的例子。有 12 个音调间,距离 C4 基础音调的音程(Interval)和 大致频率比(C4: 当前音调,精确小数点后一位)如下:
| C4 | C♯ D♭ |
D | D♯ E♭ |
E | F | F♯ G♭ |
G | G♯ A♭ |
A | A♯ B♭ |
B | C5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 261.63 (0) |
277.18 (+1) |
293.66 (+2) |
311.13 (+3) |
329.63 (+4) |
349.23 (+5) |
369.99 (+6) |
392.00 (+7) |
415.30 (+8) |
440.00 (+9) |
466.16 (+10) |
493.88 (+11) |
523.25 (+12) |
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
| 1:1 | 16:15 | 9:8 | 6:5 | 5:4 | 4:3 | 45:32 | 3:2 | 8:5 | 5:3 | 16:9 | 15:8 | 2:1 |
那么,这一发现有什么作用呢?
它的作用,体现在 创造新的音色。