2.3.1 辐射亮度（Radiance）& 色温（Color Temperature）& 颜色的量化

辐射亮度（Radiance） 也被称为辐亮度，是用于描述指定辐射源，单位方向上辐射强弱的客观物理量。

辐射度学（Radiometry） 和 光度学（Luminosity），都是对电磁辐射能量进行计量的学科。不同之处在于，辐射度学是物理电磁波能量角度的客观计量，光度学是人眼视觉的主观因素后的相应计量。因此，相比于之前在颜色三要素里提及的 光亮度（Luminance），辐射度学的 辐射亮度（Radiance） 其实才更贴近光亮度的物理本质。

而人们是如何通过辐射度学对能量的定义，将光的波长和颜色对应起来的呢？这就需要提到色温的概念了。

色温（Color Temperature） 是由物体本身的黑体辐射决定的一个物理量，计量单位为 K（开尔文温度）。它被定义为，绝对黑体从绝对零度（－273.15℃）开始加温后所呈现出的颜色。由于颜色本身就是一个主观量，而颜色又是由光的波长决定的，不同的色温本质上对应的是不同波长的光。所以，如果我们将色温这个纯粹的辐射度学概念延伸应用到了色彩领域，就能利用色温代表意义本身，建立起两个体系之间的联系了。

辐射度学与光度学的单位转换

同光亮度，辐射亮度的计算也需要依赖于辐射强度度量。 辐射强度（Radiant Intensity） 是用于表示光源给定方向上单位立体角内辐射通量的物理量，单位是瓦特每球面度（ $W/sr$ ）。辐射通量（Radiant Flux）是指单位时间内通过某一截面的辐射能，位是瓦特（ $W$ ）。

记辐射亮度为 $L_{\mathrm {e}}$ ，辐射强度为 $I_{\mathrm {e}}$ ，辐射通量为 $\Phi _{\mathrm {e}}$ ，辐射照射度 $E _{\mathrm {e}}$ 。那么四者间的关系为：

${\displaystyle \begin{aligned} &{I _{\mathrm {e}}} = {\frac {\mathrm {d} \Phi _{\mathrm {e} }}{\mathrm {d} \Omega} \rightarrow \Phi _{\mathrm {e}}} = \int _{\Sigma } I_e \cdot {d} \Omega \\ &E_{\mathrm {e}} = {\frac {\mathrm {d} \Phi _{\mathrm {e} }}{\mathrm {d} A}} \rightarrow \mathrm {d} ^{2}\Phi _{\mathrm {e} } = \mathrm {d} E_{\mathrm {e}} \cdot \mathrm {d} A \\ & L_{\mathrm {e}} =\frac {\mathrm {d} ^{2}\Phi _{\mathrm {e} }}{\mathrm {d} A\,\mathrm {d} \Omega \cos \theta } =\frac {\mathrm {d} E _{\mathrm {e} }}{d \Omega \cdot \cos \theta } \\ \end{aligned} }$

公式中，辐射源面积为 $A$ ，立体角为 $\Omega$ ，照射角为 $\theta$ ，概念基本等同光亮度公式同位参数。

显然，光亮度和辐射亮度的差异只在于参考系上。从有效范围上看，光亮度属于辐射亮度仅考虑可见光谱区域的特殊情况。为了使两个体系能够转换，1979年第十六届国际计量大会 上，人们对发光强度单位坎德拉进行了指定。现在我们说说的一单位坎德拉，即指代发光频率为 $Hz$ 的单色光，在垂直光源表面的定向单位幅角下，测量的辐射强度。即：

$1 \ cd = 1/683 \ W/sr = 1 \ lm / sr \ \ \rightarrow \ \ 1 \ W = 683 \ lm$

因此，记光辐转化率为 $K$ ，单位为 $lm/W$ ，则 $K$ 、 $\Phi _{\mathrm {e}}$ 与 $\Phi _{\mathrm {v}}$ 存在两者之间的转换关系：

${\displaystyle \Phi_v = K \cdot \Phi_e \quad \quad K = 683 \ lm/W}$

带入光亮度 $L_{\mathrm {v}}$ 与辐射亮度 $L_{\mathrm {e}}$ 的公式，可得：

${\displaystyle L_{\mathrm {v}} = K \cdot L_{\mathrm {e}} }$

如此就可以通过 $K$ 来完成，辐射度学和光度学间计量的转换了。

我们知道光度学中的不同颜色，本质是波长的不同。而不同的波长在辐射度学中，则代表为不同的能量密度。只要求得对应颜色光的能量密度，就能反向推算对应颜色光的波长了，进而可以将感知到的颜色用实际物理量标定。 借此，以主观感受的客观测量值，人为映射量化建立联系。

至于能量密度的测定，则可以经由物理学体系的黑体辐射定律揭示而出。

从色温到颜色 - 颜色的波长标定

色温（Color Temperature） 是由物体本身的黑体辐射决定的一个物理量，计量单位为 K（开尔文温度）。它被定义为，绝对黑体从绝对零度（－273.15℃）开始加温后，在辐射到达指定复合波情况时所具有的温度。

1900年在德国物理学会上，著名的德国物理学大师 马克思·普朗克（Max Karl Ernst Ludwig Planck，1858 - 1947），公布了自己在电磁波能量问题上的假设，这就是在物理学界影响深远的《论正常光谱中的能量分布》报告。报告的细部由同年普朗克发表的两篇论文组成，分别是《关于维恩频谱方程的改进论》(On an Improvement of Wien's Equation for the Spectrum) [23] 和《关于正常光谱中的能量分布的理论》（On the Theory of the Energy Distribution Law of the Normal Spectrum）[24] 。这两篇理论统一了之前由“紫外灾变”问题分割的，高频有效的维恩位移定律和低频有效的瑞利-金斯公式，并直接促成了量子理论的奠基和近代物理学革命。

记 $\lambda$ 代表电磁波长，$v$ 代表 $\lambda$ 的频率， $T$ 代表色温， $c$ 为光速，普朗克黑体辐射定律（Planck's law｜Blackbody radiation law） 的能量密度公式提出：

${\displaystyle \begin{aligned} u_{\lambda }\ (\lambda,T) ={\frac {8\pi hc}{\lambda^{5}}} \cdot {\frac {1}{e^{\tfrac{hc} {\lambda kT}}-1}} ={\frac {4\pi}{c}} \cdot I_e (v) ={\frac {8\pi hv^3}{c^{5}}} \cdot {\frac {1}{e^{\tfrac{hv} {kT}}-1}} ={u_{v }\ (v,T)} \\ \end{aligned} }$

公式中， $c$ 为光速，

有 $h$ 为 普朗克常数 取 $(6.62607015 \cdot 10^{-34})\ J\cdot s$ ，国际计量大会通过决议值，

有 $k$ 为 玻尔兹曼常数 取 $(1.380649 \cdot 10^{-23})\ J/K$ ，国际计量大会通过决议值，

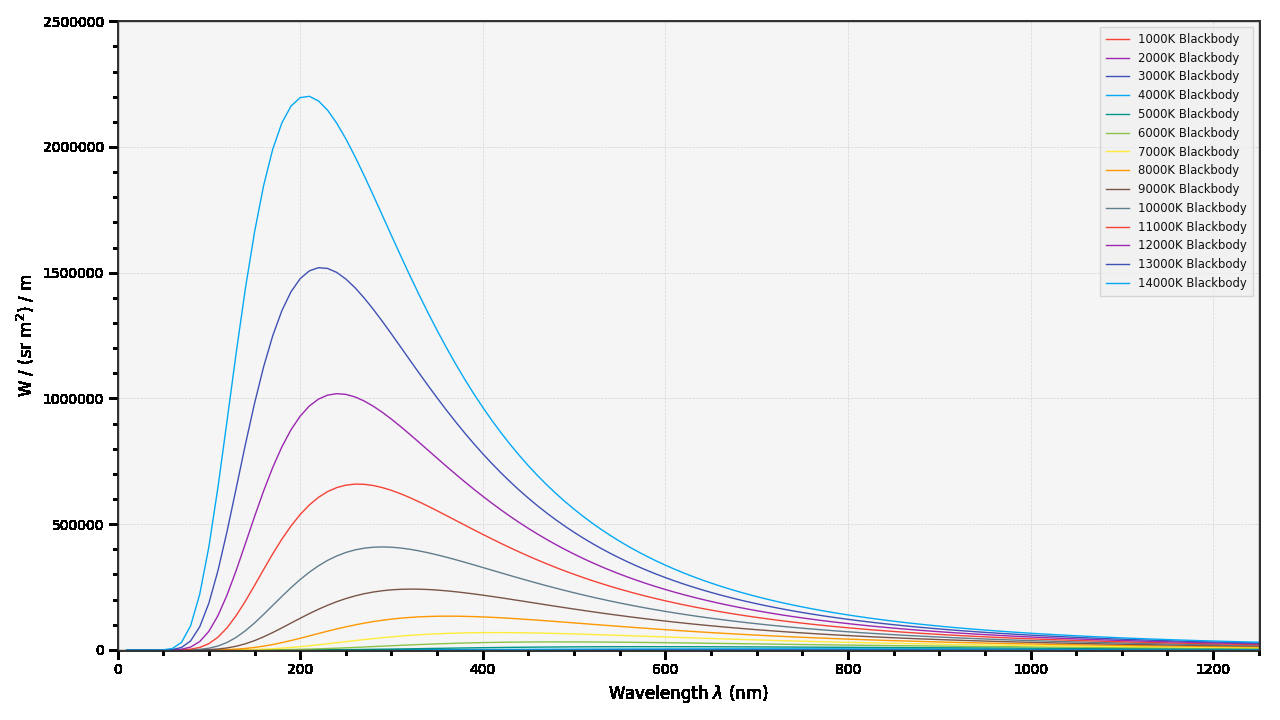
当已知黑体辐射源，其单位立方体所含能量与光波长关系如下图所示：

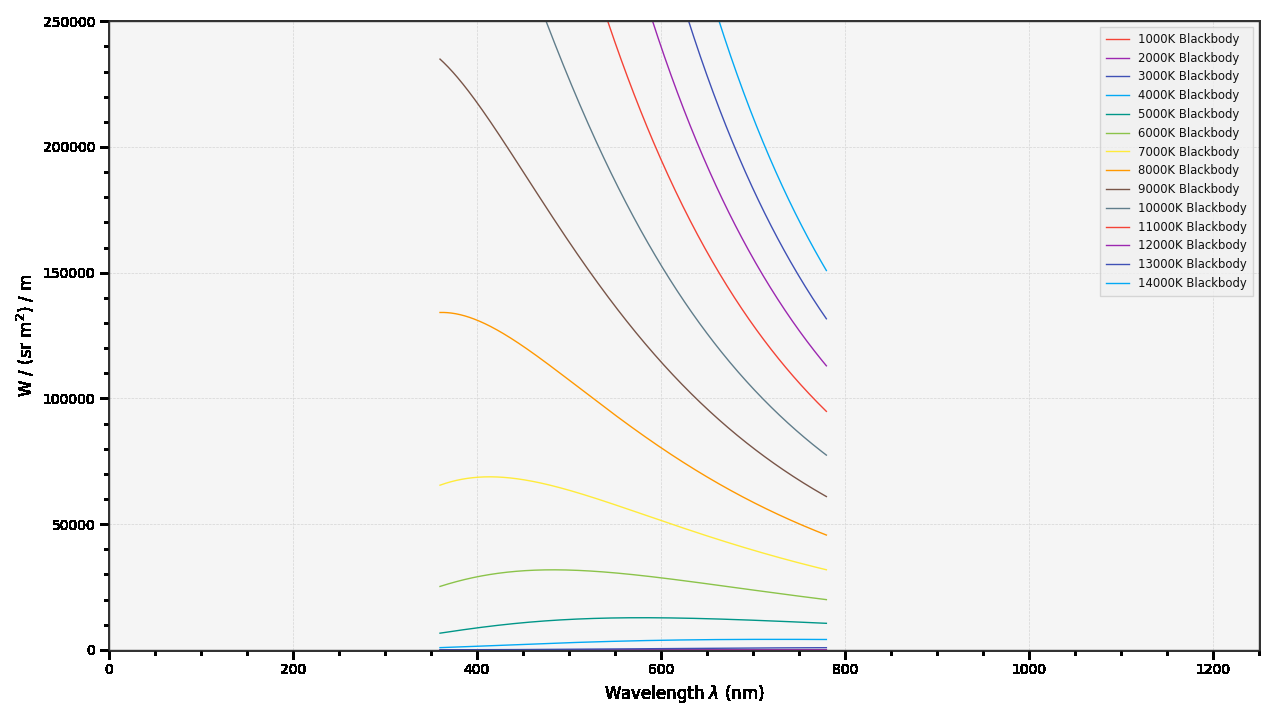
图上能明显看到，当物体处于不同色温时，其黑体辐射的总能量被分配到了不同波长光波携带。最终辐射波的情况，则是由不同区段的波长叠加而成，其叠加的强度则和对应波长携带的能量强度正相关。我们取 360nm - 780nm 可见光谱（Visible Spectrum） 范围，那么上图就有如下的展示了：

显然，色温高于 5000k 的物体在短波段出现了极大的富集程度，色温低于 5000k 的物体则是长波较为密集。所以自然界中的高温物体在人眼观察中往往偏向蓝白色，相关色温低温的物体则多呈现橙红色。

记色温为 $T_{0}$ ， $T_{0}$ 对应的颜色为 $C_{0}$ 光亮度 $L_{0}$ ， $C_{0}$ 对应可见光范围总辐射强度为 $I_{e}$ ，光强度 $I_{v}$ 。单位面积辐射能为 $Q$ ，存在映射函数 $Mapping(C_0,\ L_0) = Q$ 。

据电磁波辐射能公式有：

${\displaystyle \begin{aligned} &Q = {L_e} \cdot dA = {\frac {1}{K}} \cdot {I_v} \cdot {\frac {\mathrm {d} \Phi _{\mathrm {v} }}{\mathrm {dA^2} \cos{\theta }}} \cdot dA = \int _{360nm} ^{780nm} u_{\lambda }\ (\lambda,T_0) \cdot {d} {\lambda} \approx \sum _{360nm} ^{780nm} u_{\lambda }\ (T_0) \cdot {\lambda} \end{aligned} }$

取 $1\ sr$ 单位发光 $1\ lm$ 单位光通量，即 $I_{v} = 1\ cd$ 。

假设所有区段的电磁波在传播方向上相同，且法线方向。则上式可化为：

${\displaystyle \begin{aligned} &Q = {\frac {1}{K}} \cdot {L_v} \cdot {dA} = {\frac {1}{K}} \cdot {\frac {I_v}{dA}} = \sum _{360nm} ^{780nm} u_{\lambda }\ (T_0) \cdot {\lambda} \ \ \rightarrow \ \ Q = {L_v} \cdot \sum _{360nm} ^{780nm} {\frac {u_{\lambda}}{I_v}} \lambda \cdot {\mathrm K } = {L_v} \cdot \sum _{360nm} ^{780nm} {\frac {u_{\lambda}}{I_e}} \lambda \\ \end{aligned} }$

那么带入映射函数，我们就有：

${\displaystyle \begin{aligned} &Mapping(C_0, L_0) = {L_0} \cdot \sum _{360nm} ^{780nm} {\frac {u_{\lambda}}{I_e}} \lambda = F(C_0, L_0) \\ \end{aligned} }$ ${\displaystyle \begin{aligned} &C_0 = Convert( \sum _{360nm} ^{780nm} {\frac {u_{\lambda}}{I_e}} \lambda ) = F( \sum _{360nm} ^{780nm} {\frac {u_{\lambda}}{I_e}} \lambda ) \\ \end{aligned} }$

可见，只要选取合适的转换函数 $F(C)$ ，我们就可以将色温为 $T_{0}$ 时对应的颜色，以 $F(C_0,\ L_0)$ 的形式表述到函数所在参考系中。因此，这个用于颜色匹配的转换函数 $F(C)$ ，就被称为 配色函数（Color-Matching Functions）。

只要能找到适合的 $F(C)$ 使颜色能够被统一的衡量，就能制定工业标准，正式开始现代化的工程实践了。