2.3.3 经典三原色函数(Trichromatic Primaries Functions)
1921 年左右,威廉·大卫·赖特(W. David Wright,1906 - 1997) [26] 与 约翰·吉尔德(John Guild,1889 - 1976) [27] 分别对光学三原色的基本度量系数进行了更为科学的测定,并分别于1928年 、1932年以论文形式发表了自己的结果。这两个实验,为 CIE 经典三原色函数(Trichromatic Primaries Functions)标准 的制定提供了极为关键的帮助。
我们将代表不同可见光波长对人眼视锥细胞的刺激程度的函数,称为色感函数,也就是选取人眼为传感器的 光谱响应函数(SPF [Spectral Response Function])。由色感函数在可见光波段所构成的曲线,称为色感曲线。由实验所拟合的三原色的色感曲线,在 435.8nm(蓝)、 546.1nm(绿)、 700nm(红)处达到最大峰值,如下图:
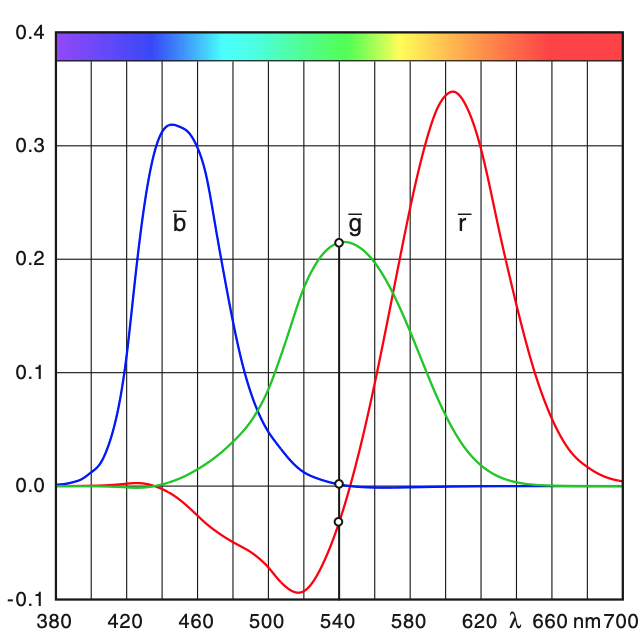
图 2-9 CIE 1931 RGB 采用的三原色色感函数
CIE 在两者实验的基础上,确定了以 光谱功率分布(SPD [Spectral Power Distribution]) 为基准的混合波三色分离函数:
R=∫0∞S(λ)r(λ)dλG=∫0∞S(λ)g(λ)dλB=∫0∞S(λ)b(λ)dλ
其中,
以 r(λ) 、 g(λ) 、 b(λ) 即为基准三原色实验测得的拟合结果的色感函数,存在关系:
∫0∞r(λ)dλ=∫0∞g(λ)dλ=∫0∞b(λ)dλ
有 S(λ) 为目标波长 λ 的光谱功率分布函数:
S(λ)=Le(λ)θ=2∘≈dAdΩd2Φe(λ)=dΩdEe(λ)
SPD 公式式中,Le 为辐射亮度, Φe 为辐射通量为, Ee 为辐射照射度。
通过这几个属于 辐射度学(Radiometry) 中的可被测量物理量,指定波长 的光线,就能被相对化表示为:
Ray(λ)=C(R,G,B)
由于 CIE RGB 所采用的改进后的配色实验,仍然存在亥姆霍兹配色实验里就存在的红光波段的负色匹配。
因此还需要进一步改进才能用于工业应用。
