3.2.2 双边滤波(Bilateral Filter)
双边滤波(Bilateral Filter) 是在高斯滤波基础上,基于 边缘保存(Edge Preserving) 滤波思想,通过一个 空间域(Spatial Domain/Domain)标准高斯滤波 和 灰度值(Gray Range/Range)朴素高斯分布 的共同作用,形成的 高斯滤波变体。
由于二维信号的高频部分,在灰度通道上体现的更为明确(本质起作用的是物理意义上的光亮度信息,人眼主要通过光亮度差异来感知物体轮廓。光亮度的多种衍生抽象,和相关概念是如何迁移数据化到计算机视觉体系内的,会在本书第三章详细讲解)。所以,双边滤波引入对灰度值的高斯,是期望提取核内灰度变化特征,来得到各频率波的核内密度分布情况。
进而对核内标准高斯滤波像素值概率密度结果进行修饰,得到 带有截面的单向滤波卷积核(Single Orientation Filter)。
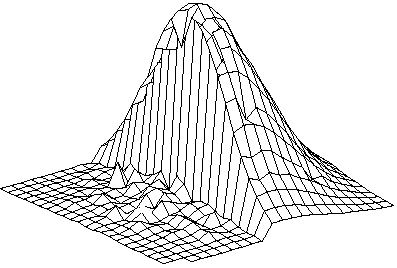
图 3-3 双边滤波经过灰度裁剪后,在轮廓边缘处的卷积核示意图 [13]
因此,双边滤波属于 混合高斯卷积核(Combined Gaussian Kernel) 滤波器的一种。我们需要分别计算 空间高斯权重(SGW [Spatial Gaussian Weight]) 和 灰度高斯权重(GGW [Gray Gaussian Weight]) 两部分,并混合权重得到最终的双边滤波矩阵。
双边滤波的混合高斯权重
空间高斯权重(SGW),也被称为 领域权重(Domain Weight),记为 ,有波动参数 。其本身代表,以选定中心点 与卷积核内相邻点的欧式距离,求得的 二维高斯概率分布 结果。即:
灰度高斯权重(GGW),也被称为 尺度权重(Range Weight),记为 ,有波动参数 。其本身代表,以选定中心点 灰度 与卷积核内相邻点灰度 的方差,求得的 一维高斯概率分布 结果。记 有:
以 表示归一化操作,记混合高斯权重为 ,则:
由于,空间高斯权重其实就是标准高斯滤波权重,因此 。我们沿用上节高斯滤波的设定,取用 大小卷积核,滤波函数记为 ,则:
而 就是一维高斯曲线的线下面积,有 ,所以:
上式中 即为高斯滤波核函数 。 可见,适用于高斯滤波 的快速算法,同样也适用于双边滤波 。
为什么通过核内频率采用朴素高斯分布,能够达到裁切的目的呢?这是因为,当卷积核目标中心点处于图像中物体的轮廓位置附近时,卷积核内的频率分布会出现相对非轮廓区域更为强烈的波动。 而高斯分布,即正态分布,恰恰是一种常用的放缩范围内数据波动的手段。
在标准高斯滤波中,我们通过多维高斯,粗浅的处理了整体数据上的波动性。这种处理方式,相当于将图像经过二维傅里叶变换得到的空域(SD)数据和频域(FD)数据,统一按照全通道空域的像素均值分布情况进行了概率平均。忽略了频域本身所具有的实际意义。而灰度值高斯的作用,就是 间接 的达成抽象频域数据波动特征的目的。
通过降低 取值,放大核内频率差异情况。增强高频部分的权重,衰减低频占比。因此,对于双边滤波来说:在满足取 越小,波动性越强越激烈,图片越尖锐;反之 越大,波动性越弱越平缓,图片越模糊的同时;取 越大,高低频差异缩减,边缘越模糊;反之 越小,高低频差异被放大,边缘越清晰。
双边滤波的 GLSL 渲染程序片
现在,我们可以依据理论来做 GPU 的动态管线程序片封装了。
首先,我们需要定义 顶点程序片(Vertex Shader)。通过该程序片指定 GPU 的绘制区域,以及纹理与物体的点位映射。由于我们是对整个视窗界面进行处理,所以可以采用对传入的顶点数据进行坐标变换的方式,来求得顶点映射的纹理坐标,减少少量数据通信:
attribute vec3 position;
varying vec4 fs_position;
varying vec2 fs_texcoord;
void main()
{
fs_position = vec4(position.x, position.y, position.z, 1.0);
fs_texcoord = (position.xy + vec2(1.0, 1.0)) / 2.0;
gl_Position = fs_position;
}
没有太多操作,因为关键的部分在 像素程序片(Pixel Shader/Fragment Shader) 上:
precision mediump float;
varying vec4 fs_position;
varying vec2 fs_texcoord;
uniform vec2 pixel_bias;
uniform mat3 gaussian_matrix;
uniform float gaussian_range;
uniform sampler2D target_texture;
float variance(vec3 c1, vec3 c2){
vec3 temp = c2 - c1;
return temp[0] * temp[0] + temp[1] * temp[1] + temp[2] * temp[2];
}
void main()
{
vec3 output_;
vec4 color_center = texture2D(target_texture, fs_texcoord.xy);
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
vec2 bias = vec2(i-1, j-1) * pixel_bias;
vec4 color_sample = texture2D(target_texture, fs_texcoord.xy + bias);
float grey_variance = variance(color_center.rgb, color_sample.rgb) / (2.0 * gaussian_range * gaussian_range);
float range_weight = exp(-grey_variance);
output_ += color_sample.rgb * gaussian_matrix[i][j] * range_weight;
}
}
gl_FragColor = vec4(output_, 1.0);
}
完成对算法求和过程的迁移。传入的 高斯算子 gaussian_matrix 和 相邻像素归一化的偏移距离 pixel_bias 的操作,只需要在执行前由 CPU 计算一次即可。而 灰度高斯权重 gaussian_range 涉及到实际采样,需要直接传入。由于采用 Web 展示,此处方法以 JavaScript 语法实现:
function pixel_bias(width, height) {
return new Float32Array([
1.0 / width, 1.0 / height
]);
}
function calculate_gaussian_kernel(step, delta) {
let n = step * 2 + 1;
let kernel = new Float32Array(n * n);
let factor_1 = 1.0 / (Math.sqrt(2.0 * Math.PI) * delta);
let factor_2 = 1.0 / (2.0 * delta * delta);
let normalize_div = 0;
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
let diff = Math.pow(i - step, 2) + Math.pow(j - step, 2);
kernel[j + n * i] = factor_1 * Math.exp(-diff * factor_2);
normalize_div += kernel[i];
}
}
for (let i = 0; i < kernel.length; i++) {
kernel[i] /= normalize_div;
}
return kernel;
}
如上,双边滤波需要固定计算的部分,和标准高斯滤波并无不同。工程中,仅在像素程序片的实现上存在差异。
同理,双边滤波也是可以使用 线性插值(Linear Sampling) 代替部分采样,来进行加速。和标准高斯滤波一样,只需要略微调整像素程序片(Pixel Shader/Fragment Shader)的实现:
precision mediump float;
varying vec4 fs_position;
varying vec2 fs_texcoord;
uniform vec2 pixel_bias;
uniform mat3 gaussian_matrix;
uniform float gaussian_range;
uniform sampler2D target_texture;
float variance(vec3 c1, vec3 c2){
vec3 temp = c2 - c1;
return temp[0] * temp[0] + temp[1] * temp[1] + temp[2] * temp[2];
}
void main()
{
vec4 color_center = texture2D(target_texture, fs_texcoord.xy);
float gauss_factor = gaussian_matrix[0][0]+gaussian_matrix[0][1];
vec3 output_ = texture2D(target_texture, fs_texcoord.xy ).rgb * gaussian_matrix[1][1];
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
vec2 bias = vec2(1-2*i, 1-2*j) * pixel_bias;
vec4 color_sample = texture2D(target_texture, fs_texcoord.xy + bias);
float grey_variance = variance(color_center.rgb, color_sample.rgb) / (2.0 * gaussian_range * gaussian_range);
float range_weight = exp(-grey_variance);
output_ += color_sample.rgb * gauss_factor * range_weight;
}
}
gl_FragColor = vec4(output_, 1.0);
}
至此,一个标准双边滤波器,和它的线性采样快速版就完成了。
双边滤波的局限性
双边滤波是否彻底的解决了高斯滤波的局限性问题呢?答案是解决了 一部分。
引入高低频分布密度权重,虽然能够处理图像中物体轮廓边缘模糊现象,达到强度可控的 边缘保存(Edge Preserving)。但由于灰度高斯权重,单一维度单一方向梯度的特点。在利用双边滤波增强高频波权重的同时,也会 增大由标准高斯滤波高频分散运动带来的干扰。这反而会让增强边缘细节过程中产生的 摩尔纹(Moire Pattern)更加显著。
为处理这个问题,我们相对放松对算力的限制。一个可行的方案是在标准高斯滤波的基础上,通过使用多个方向梯度共同作用,重新构造一个满足 非各向同性(Not Isotropic) 条件的滤波单元 (毕竟非全方位的梯度差异,还无法满足各向异性条件),来保存和引入核内像素移动和频率波传导关系。使我们能够对核内像素所占均值比重进行更为合理的分配,起到缓解效果。
这种多梯度的方式,会增强算法对图像边缘的处理能力,保存边缘的同时增强细节。因此也被称为 边缘锐化(Edge Sharpening)。