4.2.1 算子(Operator)& 层(Layer)
算子(Operator) 和 层(Layer) 是当前各种通用神经网络模型中,最基础的组成元件。一般来说,算子用于表示模型中的数学运算,而层用于组织模型中的算子。我们通常将单一的数学函数,抽象为一个算子。
需要注意的是,两者皆为 工程概念。
算子(Operator)
算子(Operator) 本身仅代表基础运算。因此,既可以是一对一的输入输出,也可以是多对多的输入输出,可以是有状态的或无状态的,也可以是可微的或不可微的。而在使用中,类似 ReLU 等激活函数,或 Dropout 之类的损失函数,都可以被定义为算子,以方便过程中直接使用。
有状态算子在计算输出时,会对前次计算的结果进行 一定程度的 抽象记录,从而 保存以前的状态。循环神经网络 (RNN) 中的循环单元(Recurrent Unit)就属于有状态算子。无状态算子在计算输出时不需要记住以前的状态,卷积神经网络 (CNN) 中的卷积算子就属于无状态算子。
可微算子的导数可以计算,这使得它们可以用于训练神经网络。例如,线性算子和非线性算子都是可微的。不可微算子的导数不能计算,这使得它们不能用于训练神经网络,但能够做最终汇总所用。例如,Maxout 算子就是一个不可微算子。
可见,算子本身是灵活的,基本作用等同于一次单一的数学运算,而不在意具体类型。由它构成了 整个神经网络中最基础的 “加减乘除” 功能。
层(Layer)
层(Layer) 是由一组算子组成的,神经网络基本组成部分。这些算子共同执行一个特定的任务。例如,卷积层(Convolution Layer) 由一组卷积算子组成,这些算子共同执行卷积操作。池化层(Pooling Layer) 由一组池化算子组成,这些算子共同执行池化操作。
根据不同的出发点,层可以进行 非单一化 的分类。
按照 功能特性,可以分为 卷积层(Convolutional Layer) 、 全连接层(Fully Connected Layer) 、 池化/下采样层(Pooling Layer/Subsampling Layer) 、 上采样层(Upsampling Layer)。
顾名思义,卷积层即卷积算子参与运算的层级,全链接层即采用连接函数精简参数的层级。同理,池化/下采样层即采用 传统/非传统 的下采样算法(Subsampling Function),进行输入数据精简的层级,而上采样即是采用 传统/非传统 的上采样算法(Upsampling Function)对数据进行扩充的层级。这种命名法的好处是 直指功能,缺点是不太好区分流程中位置。需要根据对模型的熟悉程度和经验,来确定实际生效的阶段。
按照 数学特性,可以分为 线性层(Linear Layer) 或 非线性层(Nonlinear Layer),两种类型。线性层由一组线性算子组成,这些算子共同执行线性变换。例如,全连接层就是一个线性层。非线性层由一组非线性算子组成,这些算子共同执行非线性变换。例如,卷积层就是一个非线性层。
按照 网络特性,可以分为 前馈层(Feed Forward Layer) 或 循环层(Recurrent Layer)。前馈层中的信息只从输入流向输出。循环层中的信息可以从输入流向输出,也可以从输出流向输入。这种分类方式常被使用在 自注意力网络(Transformer) 的层单元中,也可以适当的用来描述其他类型深度神经网络中的层划分。不过,由于如 CNN、RNN 相较于 Transformer 的层级特点相对单一,所以一般不会这么使用。例如,卷积神经网络 (CNN) 中的卷积层就是一个前馈层,循环神经网络 (RNN) 中的循环单元就是一个循环层,不如直接以数学特性表述的准确。
不过,最常见的分类方式,还是直接以层所处神经网络(Neural Network)位置进行划分,称为 经典基础层类型(Classic Base Layer Type)。
经典层分类(Classic Base Layer Type)
经典基础层类型,将层分为三类,分别是:输入层(Input Layer) 、 隐藏层(Hidden Layer) 、 输出层(Output Layer)。这种分类非常直观:
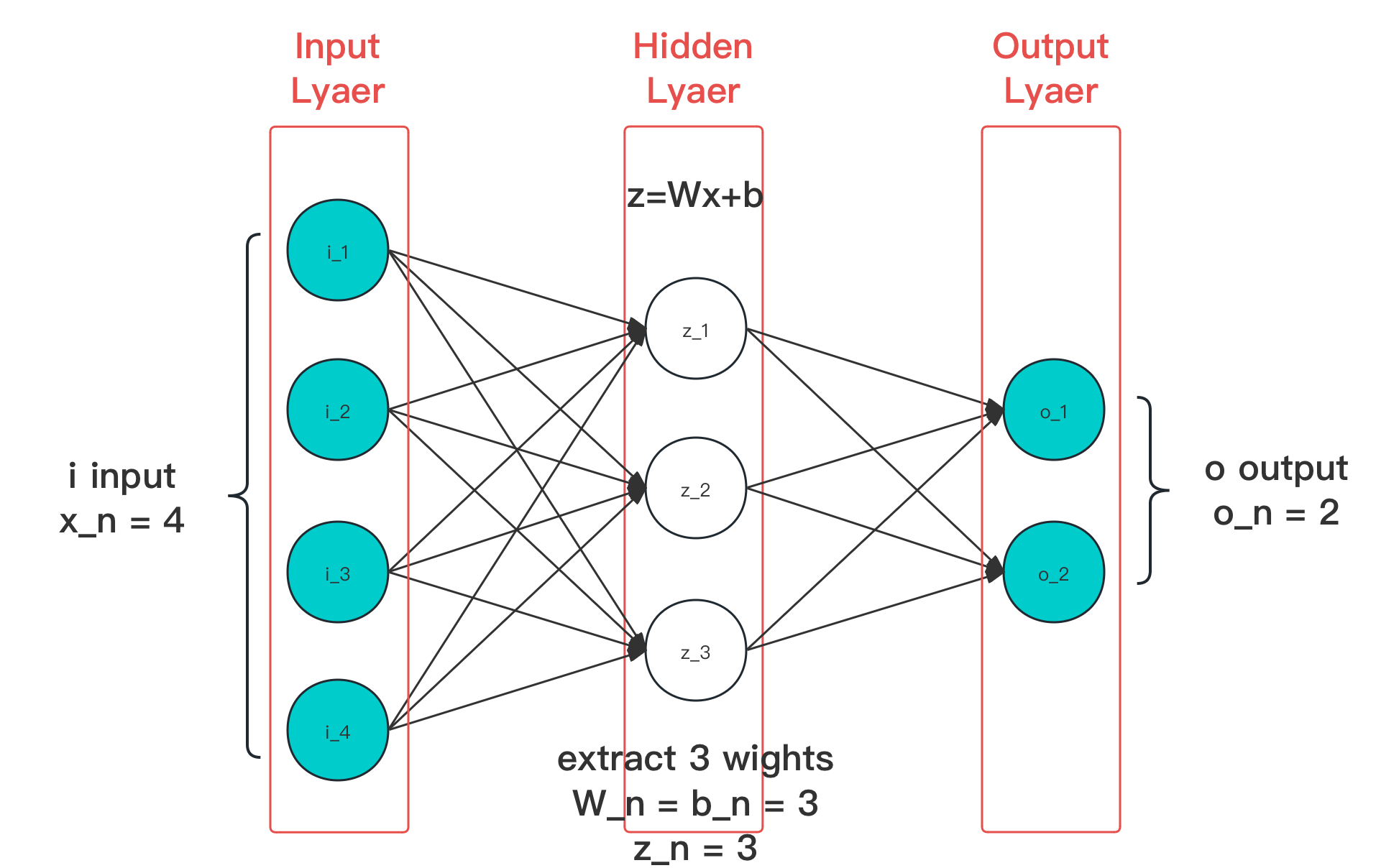
图 4-5 经典层分类在简单神经网络中位置示意图(切片)
输入层(Input Layer) 是一个神经网络的 输入节点集合(Input Nodes Set),负责接收外部传入的数据。显然输入数据的维度,决定了输入层节点的数量。如图,假设我们传入的训练用样本中,每一个样本数据皆为 向量的话,那么输入层的节点就同样有 个。
隐藏层(Hidden Layer) 是一个神经网络的 特征提取节点集合(Feature Extract Nodes Set),负责将输入层经过激活函数处理后的数据,交付权重运算,得到抽象后的 特征向量(Feature Vector) 输出。如图,这里我们指定抽取的特征为 向量,因此需要 个隐藏层节点。由于本身处于神经网络内部,所以被称为隐藏层。 该层也是反向传播(BP)算法,起到主要作用的层级。
输出层(Output Layer) 则是神经网络的预测结果 输出节点集合(Prediction Output Nodes Set),负责将临近的隐藏层输入,通过连接函数(Connection Function)转换为最终的预测结果输出。也就是将抽象的特征向量,转化为实际当次时期(epoch)预测结果的关键层。
通常情况下,一个神经网络只会有一个经过专门设计的输出层。输出层的结果将会与样本集中该样本的标注结果,一同作为损失函数的输入做损失计算,并以此迭代权重变化。
图中,我们期望的预测输出是个 的结果向量,向量的维度依赖于对比集的标注。此时,输出层就需要采用 个节点,来接收前一级隐藏层的输入(例子只有一层隐藏层)。
所以综合而言,在工程上,算子常常是以最小的 方法单元(Method Unit) 而存在,层中节点相当于最小 执行单元(Operation Unit)。层则相当于由一系列算子按照一定的处理顺序,组成的 任务单元(Task Unit)。而模型(Model)则是由一系列层按照既定目标排列组合,形成的 作业流水线(Process Pipeline)。