4.3.2 Tanh
迭代公式:
sinh(x)cosh(x)δ(x)=tanh(x)=2ex−e−x=2ex+e−x=cosh(x)sinh(x)=ex+e−xex−e−x
图像:
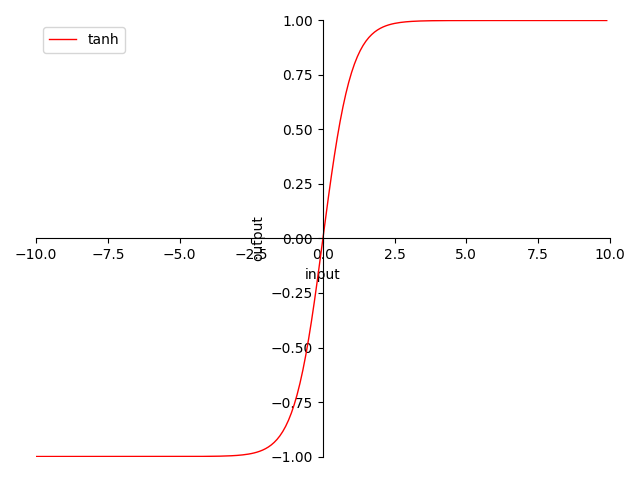
图 4-10 Tanh 函数图
特性:
- 0 为中心(zero-centered)
- 输出范围在 [−1, +1] 之间,输出值域对称
- 当输入在 (−∞, −2.5] 或 (−∞, −2.5] 时,Tanh也会面临梯度趋 0 问题(过饱和问题)
- 指数计算,较为消耗资源
不难看出 Tanh(x)=2⋅Sigmoid(2x)−1 。本质上来讲 Tanh 属于Sigmoid 的一种变体,尝试通过平移拉伸变换,来解决 Sigmoid 的非原点对称问题。虽然能够处理梯度堆积带来的影响,但是 tanh 同样不能处理相较于堆积更为严重的梯度消失问题。这也是饱和类激活函数的通病。
Tanh 算子化
利用 C 语言实现对算子的封装,有:
#include <stdio.h>
#include <math.h>
double tanh(double x) {
return (exp(x) - exp(-x)) / (exp(x) + exp(-x));
}
int main() {
double x = 0.5;
double y = tanh(x);
printf("The tanh of %f is %f\n", x, y);
return 0;
}
运行验证可得到结果:
The tanh of 0.500000 is 0.462117
