4.6.2 优化算法的优化-应对震荡
常用的减震算法,比较容易想到的就是利用 阻尼运动特性 和 加速度,即 动量(Momentum),来减小离散瞬时值的影响。因此,先贤们首先想到的就是梯度迭代动量化。
标准动量(Standard Momentum)
迭代公式:
标准动量(Standard Momentum) 是在原有计算权重迭代基础上,通过引入上一次变化值情况,来强化梯度延方向变化趋势。即 SGD/BGD/MBGD + Momentum。 这样做可以使得梯度方向不变的维度,权重迭代速率加快,而方向发生改变的维度,更新速度变慢。并且由于速度此时变化是和 之前状态 有关系的,就不会发生“指向突变”的情况,有助于减小震荡和跃出鞍点。
超参数 被称为 阻尼系数,或遗忘因子。一般取 ,表示经验重要程度。
然而,单纯的动量处理却也存在其他问题。最明显的就是,因为动量叠加,没有修正逻辑的纯动量叠加,会导致每一次的轻微误差也随着时间一起叠加,导致当前时刻 时,实际梯度变化速率要远大于实际值,阻尼因子设定过小和初速度过大都可能会久久不能收敛。所以,在动量化的基础上,我们更希望能够有修正方法来减小误差的累积。
幸运的是 Nesterov Y. 在1983年提出的 NAG 很好的解决了这个问题。
涅斯捷罗夫梯度加速(NAG [Nesterov Accelerated Gradient])
迭代公式:
涅斯捷罗夫梯度加速(NAG [Nesterov Accelerated Gradient]) 较标准动量化处理来说,用来计算当前梯度方向的时候,计算 损失函数(Loss) 采用的是基于当前上一次梯度变化值预测的,当前状态下,下一次可能的维度权重。以这个预测的维度权重来计算当前位置的方向梯度变化,来修正动量化算法。这样,当我们计算当前 时梯度变化速度的时候,就可以从一定程度上避免掉误差堆积导致的问题。
这里借用一下 Hinton 课程 [17] 中的图来说明效果:
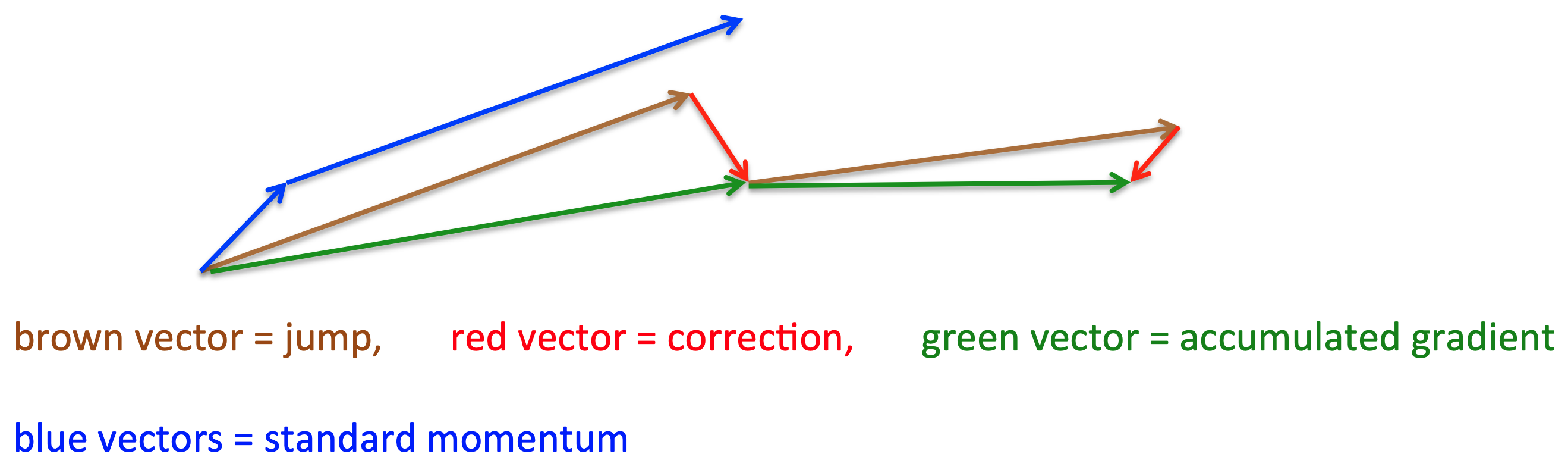
图 4-36 NAG 加速作用过程示意图[17]
可以看出,蓝色(blue vector)是 标准动量 的过程,会先计算当前的梯度,然后在更新后的累积梯度后会有一个大的跳跃。绿色是 NAG 会先在前一步 棕色(brown vector) 的累积梯度上有一个大的跳跃,然后衡量梯度做 红色(red vector) 修正偏移。
这种预期的更新可以避免我们走的太快。