3.4.3 光流仿射修正(PROF [Affine Prediction Refinement With Optical Flow])
BDOF 技术的引入,让音视频编解码工程能够进一步提高传输过程的数据压缩比。但由于仍然依托于分块和分块内小块(也是前文的梯度卷积核),当出现块的偏移、扭转、错切等情况时,像素位置的微小变动则会被此类变化成倍的放大误差。所以,还需要 适当的修正。
我们知道,音视频编解码规格(如 H.264、H.265、H.266)中,分块的子块也是存在类似的情况的。我们为了处理问题,采用的是 基于控制点运动矢量(CMVP [Control Point Motion Vector])的子块仿射运动补偿(AMC [Affine Motion Compensation]),并在 H.266 中根据目标子块大小衍生出了 高级运动矢量预测(AMVP [Advanced Motion Vector Prediction])的仿射模式,和 混合预测(Merge)的仿射模式。通俗理解,即通过相邻帧的相同块内子块的仿射变换,来映射原子块区域的对应关系。
但子块控制点的运动是远大于像素运动的,那么同样的情况发生在更小的尺度上,是否还能达到效果呢?
答案是可以的。
在 LK 条件下局部光流趋同性,决定了像素光流的差分补偿对分块只需要单次计算即可。那么对于子块来说,只用在原有仿射运动补偿(AMC)的基础上,对块内像素额外附加 光流补偿值(OFC [Optical Flow Compensation]) 即可。
记分块 m 有,中心点 Kxy 在全图的绝对像素位置 Kxy=(Kx, Ky) 的子块 k 。存在子块内相对位置为 pij=(i, j) 的像素点 pij 。由于子块内是不存在时差的,即时间残差 ∇tI=0 存在,则记 pij 的子块内光流补偿值(OFC)是 ΔIp ,根据基础光流公式就有:
ΔIp=∇pI⋅Δv⃗p + ∇tI=∇pI⋅Δv⃗p
其中, Δv⃗p=(ΔVi, ΔVj) 即是点 pij 在子块 k 内的光流偏移,这个值相对子块内部中心 Kij ,在分块 m 内子块无相对变化情况时,是个恒定值,有:
ΔKp=pij−Kij=(Δi, Δj)=Δij
而根据仿射变换特点,当分块 m 发生仿射变换,其每个子块 k 的像素点内部光流偏移矢量,也会发生 等效于块中心运动补偿 的仿射变换。
因此,假设分块 m 块运动采用左上、右上、左下的三点定位(即标准三控制点),记帧 R0 到帧 R1 有块三点定位运动矢量分别为 MV⃗0 、 MV⃗1 、 MV⃗2 如下:
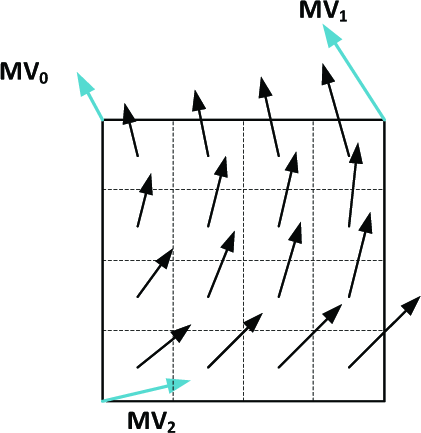
图 3-18 PROF 子块光流与块运动矢量示意图 [30]
假设分块 m 大小为 Mw×Mh ,则有块从帧 R0 到帧 R1 的位姿仿射变换矩阵 A 使得:
Δv⃗p=A⋅ΔKp=A⋅Δij=⎣⎢⎡MwMV1,x−MV0,xMwMV1,y−MV0,y,MhMV2,x−MV0,x,MhMV2,y−MV0,y⎦⎥⎤⋅[ΔiΔj]
而 ∇pI 可由子块 LK 计算等效获取,有:
Ip(i, j)∇pI(i, j)=Ip(x+Δi, y+Δj)=(∇iIp, ∇jIp)=⎩⎪⎨⎪⎧∇iIp = 2Ip(i+1) − Ip(i−1)∇jIp = 2Ip(j+1) − Ip(j−1)
所以,子块内像素的最终亮度 I^p 取值为:
I^p=Ip(x, y) + ΔIp(i, j)=∇pI(i, j)⋅Δv⃗p≈Ip(x, y) + ∇iIp⋅ΔVi + ∇jIp⋅ΔVj
上式中的 Ip 即像素点 pij=Kxy+Δij=(x+Δi, y+Δj) 的分块 m 内实际亮度预测值,可通过 BDOF 求得,也可以采用其他传统块推理方式获取。根据 PROF 的修正,BDOF 推算所得像素点的亮度将更为准确,进而在 提高压缩程度(以子块为最小压缩单位的块内冗余压缩)的同时,保证了灰度(亮度值)数据还原效果。
以上我们介绍的,就是光流法在音视频编解码过程中较为粗浅的基本应用了。这些数学工具已经通过标准化,被嵌入到了 H.266/VVC 规格中,并在同期其他竞争规格(如 AV1)的最新标准里逐步推广。而光流法的引入,无疑进一步缩减了传统音视频和机器学习之间的工程鸿沟。在可预见的未来,人工智能模型流水线和编解码器必然会有更深入的融合,在技术层面形成一套全新的顶层设计。这种趋势,作为音视频开发者,是不应该忽视的。
回到当前话题,在依靠光流法处理了传输格式的亮度狭时空域冗余数据后,如果能够在纯空域上,同时对随亮度传输的色度信息进行一定程度的压缩,就能更好的降低数据成本,并提升色彩还原程度,支撑更广的色域选择了。
这就是色度缩放亮度映射技术的由来。
