4.2.2 神经元(Neuron)
神经元(Neuron) 是对神经网络中的 节点(Node) 的一种,来自于仿生学的概念。上一节中我们提到的 输入/特征/输出节点集合 中的节点,都可以被称为神经元。
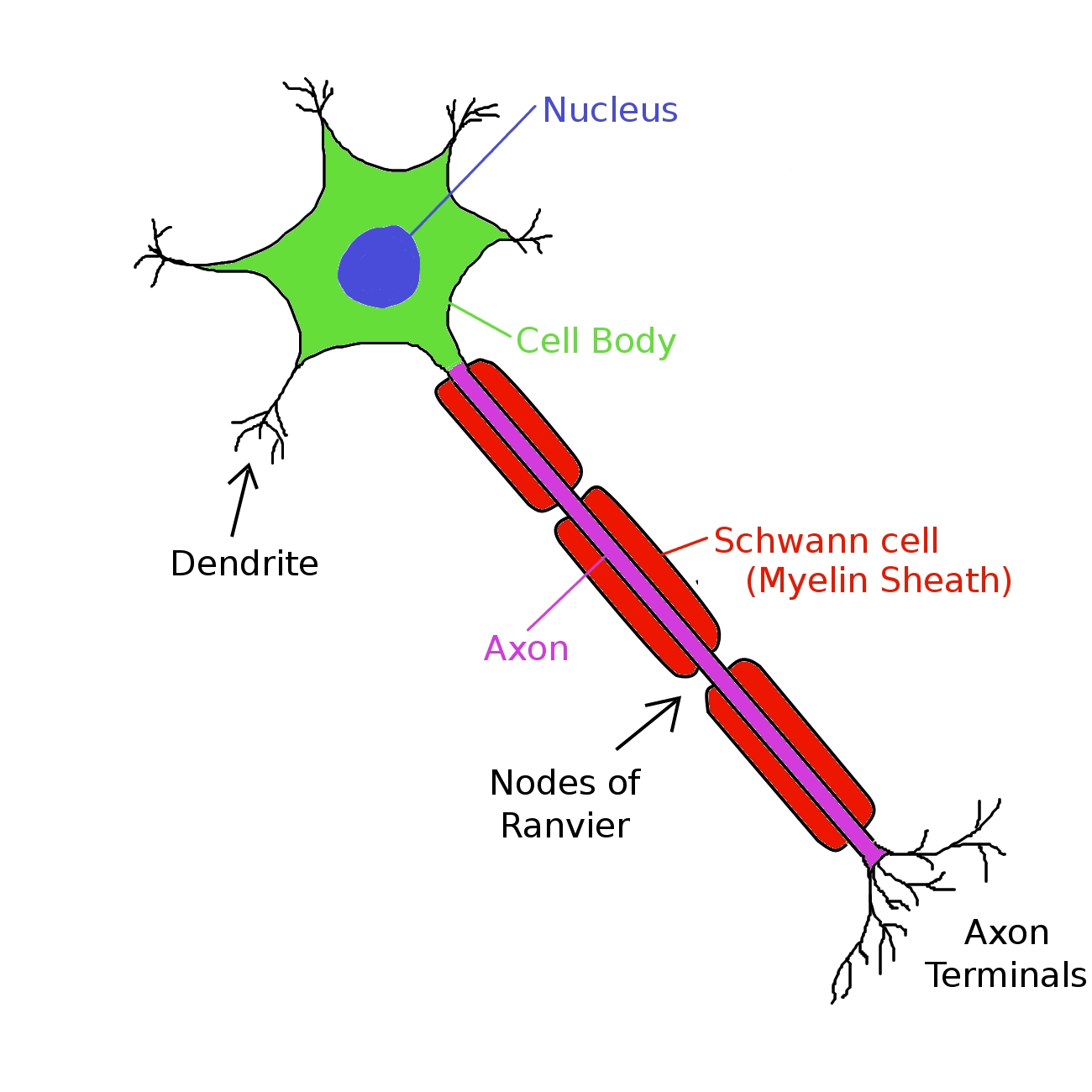
图 4-6 生物神经元示意图
生物学神经元之间的信号传递,是通过突触进行的。突触是神经元之间连接的部位。当一个神经元接收到信号时,它会释放神经递质,神经递质会穿过突触间隙,并与另一个神经元的受体结合。这种结合会引发一系列化学反应,最终导致另一个神经元产生动作电位。
这即是神经网络雏形,多层感知器(MLP [Multi-Layer Perceptron]) 的灵感来源。
在深度学习中,我们继续沿用了这一称谓,将所有设计相关层内数据计算的节点,统称为神经元。
神经元的组成
作为神经网络中最小的执行单位,神经元的成分可以统一用一个函数来说明:
上式中,
- 角标 表示当前神经元在层内的标号为 ,是一种 固定的表示 ;
- 以 表示一个输入的数值信号;
- 以 表示当前输入的 附加权重(wight),既可作为 参与训练 的层级特征权重,也可为常数 ;
- 以 表示当前输入的 附加偏移(bias),既可作为 参与训练 的层级特征偏移,也可为常数 ;
- 以 表示当前神经元的输出数值;
- 以 为当前神经元的激活函数;
可见,激活函数(Activation Function)是直接作用于神经元输入上的。
一般情况下,不论是 输入层、隐藏层,还是输出层的神经元,它们的 权重 和 偏移 ,理论上都可以参与到反向传播(BP)的参数迭代中。
但是,输出层(Output Layer) 由于本身主要作用,是 接收连接函数(Connection Function)计算预测值,不会使用到 权重 和 偏移 。我们一般为了方便起见,会将作用于输出层与前一级隐藏层之间的链接函数,整合到输出层神经元中来便于代码实现。取链接函数为 表示,有:
而 输入层(Input Layer) 一般为了工程和说明方便,会单独 只做激活,或 只传递(pass)数据并入下一级隐藏层。这使得对于输入层,神经元函数就变为了简单的:
所以,真正 完整使用 到公式的,只有 隐藏层(Hidden Layer) 中的神经元。公式:
也由此,可以被称为 隐藏层函数(Hidden Layer Function)。