3.5.1 整数离散正余弦变换(IDST/IDCT)
整数离散正余弦变换(IDST/IDCT),顾名思义,就是将原本作用于浮点域的离散正余弦变换(DST/DCT),通过适当放缩量化到整数域进行。
在本章开始时,我们曾花了大量篇幅讲解信号分析的核心算法, 傅立叶变换(Fourier Transform),并简短的辨析了一维/二维离散傅立叶变换(1D/2D-DFT)。
回顾前文。有提到,如果取任意点 P⃗(x,y) 可取 x∈[0, 1, ⋯, W] , y∈[0, 1, ⋯, H] ,只取整数位置。同时, u∈[−2U, ⋯, +2U] 、 v∈[−2V, ⋯, +2V] ,有离散 k⃗∈[k0⃗, k1⃗, ⋯, kn⃗] , n=UV=HW ,则:
SDD: f^(u,v)FDD: f(x,y)=x=0∑Wy=0∑Hf(x,y)⋅e−i(ux+vy)=U⋅V1u=−U/2∑+U/2v=−V/2∑+V/2f^(u,v)⋅Fω(x,y)
即由空域离散化(SDD)与频域离散化(FDD)共同构成空频离散化(SFD [Spacial Frequency Discrete])表达的 二维离散傅立叶(2D-DFT),如下所示:
Fω=[Fk0⃗,f^(u,v)=x=0∑Wy=0∑Hf(x,y)⋅e−i(ux+vy) ⇔Fk1⃗,⋯,Fkn⃗] f(x,y)=U⋅V1u=−U/2∑+U/2v=−V/2∑+V/2f^(u,v)⋅Fω(x,y)
虽然当时,并没有约束复平面波 Fω(x,y) 波矢 k⃗ 的方向,即方向可以是平面内任意角度与大小。但对于周期(范围)确定情况下,构成傅立叶变换的基底函数族 Fω=[Fk0⃗, Fk1⃗,⋯,Fkn⃗] ,基底函数(即原函数拆解的目标平面波组)的选取,却是可以被 一定程度约束的。
如果我们约束,取周期 T=2πn 的标准正余弦函数(Sine/Cosine),按照 四分之一周期 的步长 Step=2π 偏移得到的 Fξ(x) 和 Fη(y) 构成波矢 k⃗ 。选取沿着 x 轴方向的一维波 Fξ(x) 和沿着 y 轴方向的一维波 Fη(y) 组成的 16n 个定向复平面波 Fω(x,y) 集合,为当前函数的基底函数族。
那么,我们就能够在 补齐周期数据 后,使用 快速傅立叶变换(FFT) 来求解了。
但这样的做法,适用于分析,却并不适合冗余处理场景。
即使运用快速傅立叶变换,也仍然会有较大的算力消耗。且由于完整作用于任意数据源信号,所以不能保证基底函数族整体层面的规律性,从而无法提炼出统一的矩阵化算子。这让直接使用传统分析算法的方式,在 GPU 加速方面尽显劣势。
考虑到冗余压缩,并不要求保证数据帧完整不可分的输入,且精度也相对分析场景要求较低。如果能够适当的利用指数函数三角函数化,其本身的周期规律和标准化约束,建立基底整体的规律性,来契合傅立叶变换的性质。就能够在消减不必要参数(常量固定)并限定生效范围后,实现对离散傅立叶变化的常量化矩阵运算。建立卷积核,加速压缩过程。
因此,首选的出发点,就是 泛化离散正余弦变换(DST/DCT)到任何已知周期(范围)的数据信号源。
离散正余弦变换(DST/DCT)的泛化
沿用前文设定,记构成原信号函数 s(t) 的复指数函数 Sω(t) 有角频率(角速度)为 ωn=T2πn 。有傅立叶函数:
s(t)a^ω=N1n=0∑Na^ω⋅cos(ωt)+i⋅b^ω⋅sin(ωt)=s^(−ω)+s^(ω) b^ω=i1⋅(s^(−ω)−s^(ω))
按约束条件,信号函数波长 T=2π 做步长 Step=2π 的可变 n∈[0, N−1] 等分,使复指数函数 Sω(t)=Sω(n) 。则存在 k∈[0, N−1] 有 ωn=T2πn=N2πk=ωk 简化表示为 ω ,可对原式做三角函数离散化处理(详细推导回顾本章首节)。
当输入信号满足奇函数特性时,可得 标准正弦的离散正弦变换(DST)的傅立叶展式 为:
s(n)s^(k)=N1k=0∑N−1s^(k)⋅sin(N2πnk)=n=0∑N−1s(n)⋅sin(−N2πnk)
当输入信号满足偶函数特性时,有 标准余弦的离散余弦变换(DCT)的傅立叶展式 为:
s(n)s^(k)=N1k=0∑N−1s^(k)⋅cos(N2πnk)=n=0∑N−1s(n)⋅cos(−N2πnk)
但是,自然信号是不分奇偶的,想要将公式适用范围扩大,就需要根据正余弦傅立叶变换要求,对输入信号进行不改变原始数据的扩充调整。根据选择作为基底的标准函数正余弦的差异,人为构造 满足条件输入的方法论,被分为 离散正弦变换(DST)分解 和 离散余弦变换(DCT)分解,两套实现。
假设原信号函数 s(t)=s(n) 在 n∈Z[0, N−1] 的各节点位置,有样本采样 S∈[S0, SN−1] ,取 N=4 模拟最小子块(即实际技术被使用时的通用情况)。如图:
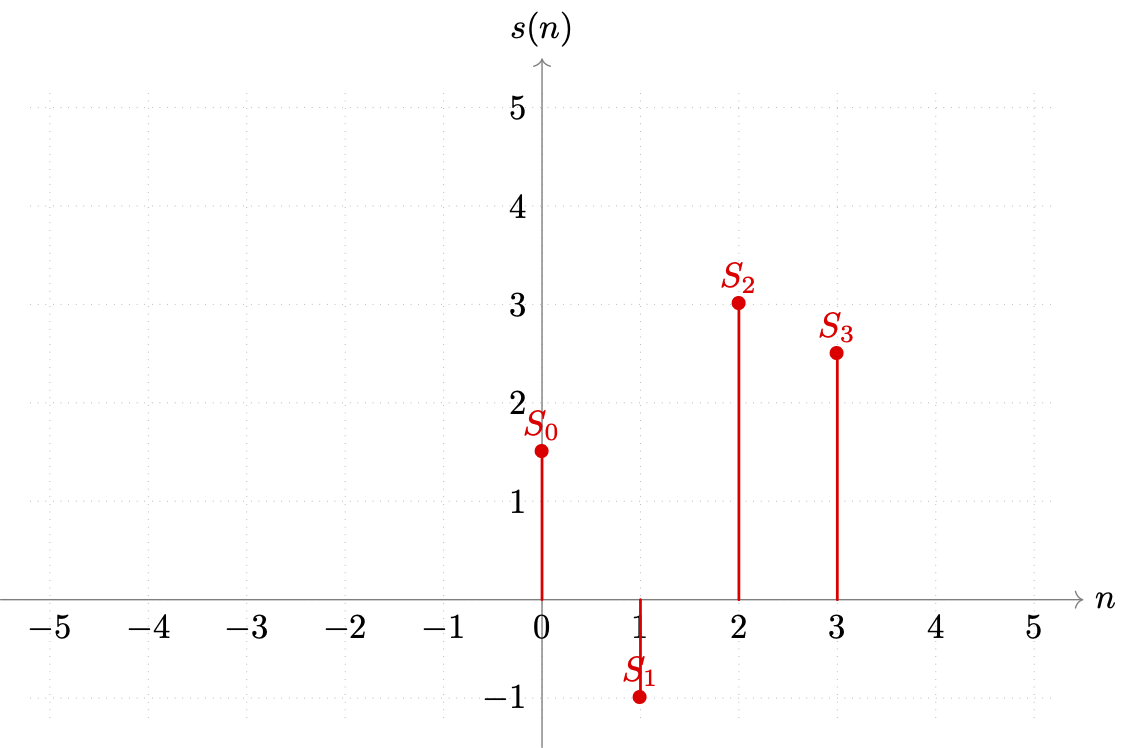
图 3-21 事例样本取值与切片索引关系图示
当目标分解为 DST 时,我们需要平移原数据 +23Step 个步长,并补充中心原点 O0 后,再做基于中心原点 O0=(0, 0) 的映射。如此才能保证,补充的映射数据和旧数据,能够组成新的等步长数据组,满足离散化的处理条件。得到如下新集合(蓝色为补充数据,红色为原数据):
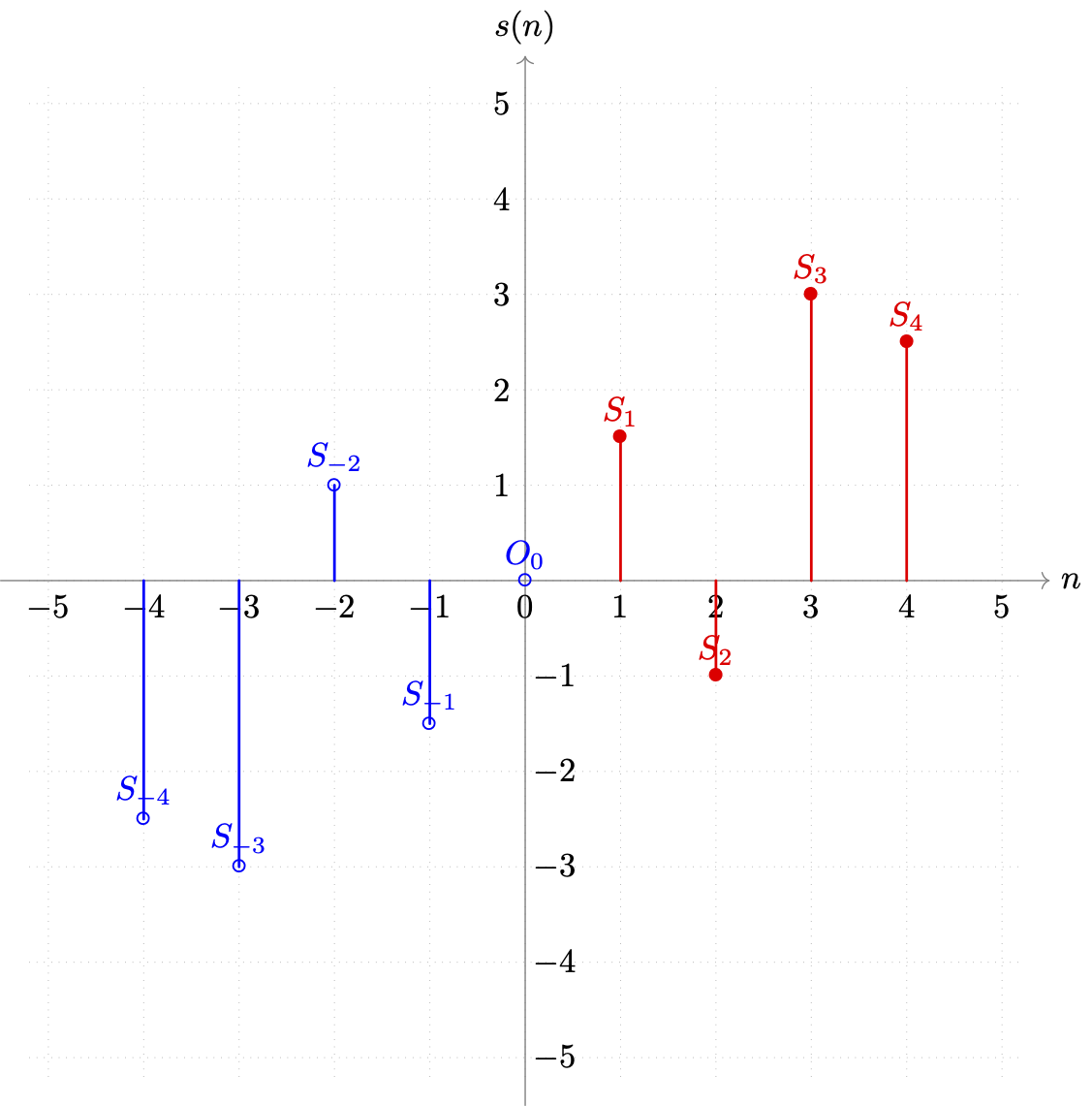
图 3-22 事例样本目标 DST 补充后与切片索引关系图示
新的样本集,数据量较原有数据翻了一倍多。但只有 轴正向的取值有意义。所以,采用 DST 类型分解,在扩充后,周期跨度都变为了 T=2N+1 ,且原离散展式 只有 n∈[1, N] 的部分是有效的。我们可以将偏移的 +1×Step 划到式中处理,则 n 的取值范围就仍然可以保持为 n∈Z[0, N−1] 。
不过考虑到 DST 目标是为了处理奇数阶信号源分解,为避免 sin(0)=0 值无意义的问题,会取 k∈[1, N] 的范围,并选用标准正弦向左移动 −21π 的偏移作为 基底正弦族。因此,为了统一,对 n 采用直接包含偏移 +1×Step 的取值,使得 n 有 n∈Z[1, N] 。需要注意这个细节差异。
当目标分解为 DCT 时,需要在基于 y=s(n) 轴对称前,先行平移元数据 +21Step 个步长。得到如下新集合(蓝色为补充数据,红色为原数据):
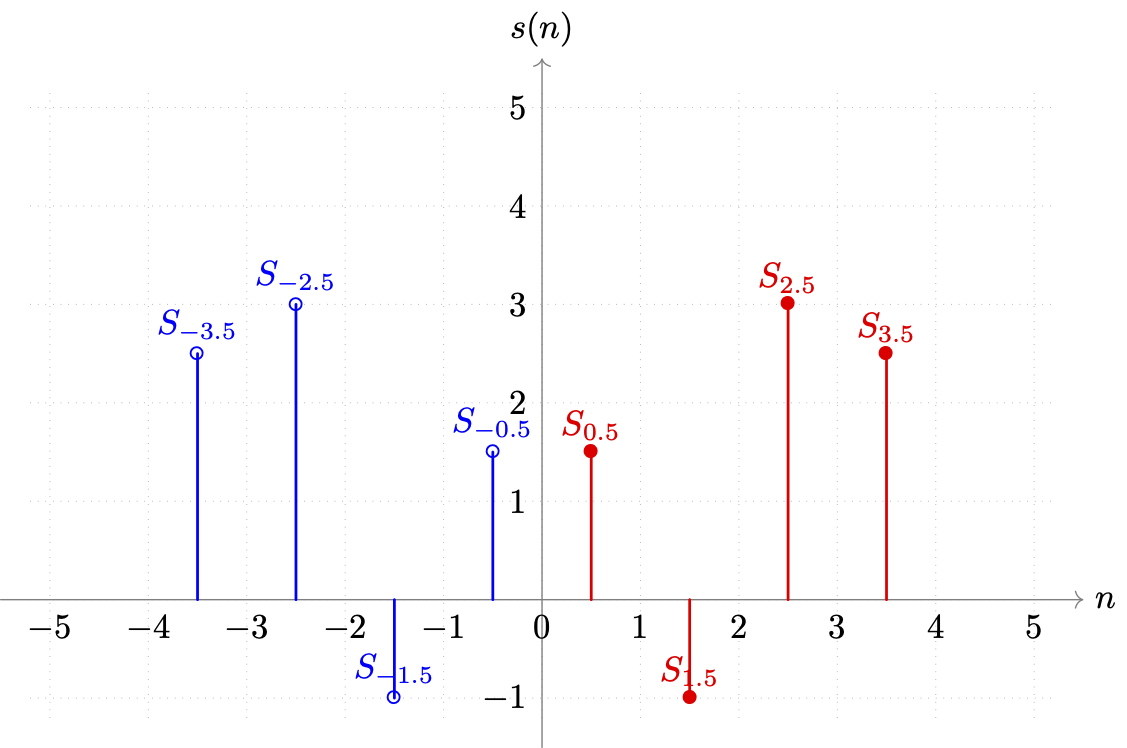
图 3-23 事例样本目标 DCT 补充后与切片索引关系图示
新的样本集,数据量较原有数据翻了一倍。同样只有 x 轴正向的取值有意义。所以,采用 DCT 类型分解,在扩充后,周期跨度都变为了 T=2N ,且原离散展式 只有 n∈[21, N−21] 的部分是有效的。而由于非整数索引 n 不利于匹配原值,我们将偏移的 +21Step 划到式中处理,则 n 的取值范围就仍然可以保持为 n∈Z[0, N−1] 。
于是,结合两种分解,有:
DST:DCT:⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧s(n)s^(k)=2N+11k=1∑Ns^(k)⋅sin(2N+12π(k−21)n)=√2N+11k=1∑N−(−√2N+11⋅s^(k))⋅sin(2N+1πn(2k−1))=2⋅n=1∑Ns(n)⋅sin(−2N+12π(k−21)n)=2⋅n=1∑Ns(n)⋅sin(−2N+1πn(2k−1))⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧s(n)s^(k)=2N1k=0∑N−1s^(k)⋅cos(2N2π(n+21)k)=√2N1k=0∑N−1(√2N1⋅s^(k))⋅cos(2Nπ(2n+1)k)=2⋅n=0∑N−1s(n+21)⋅cos(−2N2π(n+21)k)=2⋅n=0∑N−1s(22n+1)⋅cos(2Nπ(2n+1)k)
不过,由于 DCT 采用了 非整数步长,当 k=0 时并不一定有拟合的曲线使得 s^(0)=0 ,且 偶函数特点使 s^(0) 在上式中被重复计算,因此需要针对变换后的 s(n) 剔除一次的 s^(0) 均值累积,所以:
DCT∣k=0:⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧s(n)s^(k)=N1⋅s^(0)+√2N1k=1∑N−1(√2N1⋅s^(k))⋅cos(2Nπ(2n+1)k)=√2N1(√2N2⋅s^(0))+k=1∑N−1(√2N1⋅s^(k))⋅cos(2Nπ(2n+1)k))=2⋅n=0∑N−1s(22n+1)⋅cos(2Nπ(2n+1)k)
上式中,对原信号函数 s(n) 的 DST 均值常量 2N+11 拆解为 (√2N+11)2 两部分,而 DCT 均值常量 2N1 拆解为 (√2N1)2 两部分。其目的是为了,通过分别分配到各自展开式和傅立叶解上,来保证工程化后的算子,在 正逆运算上的统一。
因此,我们取:
DST:DCT:Xk=−√2N+11⋅s^(k)=√2N+11⋅s^(−k)Xk=√2N1⋅s^(k)&X0=√2N2⋅s^(k)
代入即可得到,原 离散正弦变换(DST)的工程表达式 :
DST:k∈[1, N]n∈[1, N]⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧SnXk=√2N+11k=1∑NXk⋅sin(2N+1πn(2k−1))=√2N+12⋅n=1∑NSn⋅sin(2N+1πn(2k−1))
和,原 离散余弦变换(DCT)的工程表达式 为:
DCT:k∈[0, N−1]n∈[0, N−1]⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧SnXkXk=√2N1k=0∑N−1Xk⋅cos(2Nπ(2n+1)k)=√2N2⋅n=0∑N−1Sn⋅cos(2Nπ(2n+1)k) ,k≥1=√2N2⋅2⋅n=0∑N−1Sn⋅cos(2Nπ(2n+1)k) ,k=0
这就是信号处理上经常使用的,泛化离散正余弦变换公式组。
从上面的过程中可以发现,我们在傅立叶基底函数族的选取上,实际限定了函数的相位、周期,并约束了原信号的特性。如果在初始相位和原信号特性上做调整,最终的结果也会有所差异。从数学工具角度来看,这种变化 最终会产生 8 种 DST 和 8 种 DCT 的变体,以分别应对实虚部奇偶阶数和初始相位不同时的快速计算。但由于工程化上需要力求简洁和相似(形似)的表达。因此,相对于其他几种的组合,我们最终采用的公式组中的两类,来用于各自条件输入的统一处理。
现在,GPU 加速的理论已准备就绪,我们来看算子是怎么获取的。
整数离散正弦变换(IDST)的 GPU 矩阵算子
首先,将离散正弦变换扩展到二维情况,有:
DST:Xk(u,v)k(u,v)&p(x,y)∈[(1, 1), (N, N)]=(√2N+12)2⋅p=(1,1)∑(N,N)Sp(x,y)⋅sin(2N+12u−1πx)⋅sin(2N+12v−1πy)
考虑可构成卷积核的子块最小大小为 4×4 ,则有 N=4 使上式变为:
DST:Xk(u,v)k(u,v)&p(x,y)∈[(1, 1), (4, 4)]=94⋅p=(1,1)∑(4,4)Sp(x,y)⋅sin(92u−1πx)⋅sin(92v−1πy)
如此,就可以矩阵表示 4×4 的 DST 变化为:
DST4×4:Xk(u,v)∣v=KDST⋅Sp(x,y)=[32⋅v=1∑4(32⋅u=1∑4sin(92u−1πx))⋅sin(92v−1πy)]⋅Sp(x,y)
即有:
KDST=32⎣⎢⎢⎡sin(91π)sin(93π)sin(95π)sin(97π),sin(92π),sin(96π),sin(910π),sin(914π),sin(93π),sin(99π),sin(915π),sin(921π),sin(94π),sin(912π),sin(920π),sin(928π)⎦⎥⎥⎤=32⎣⎢⎢⎡sin(91π)sin(93π)sin(94π)sin(92π),sin(92π),sin(93π),−sin(91π),−sin(94π),sin(93π),0,−sin(93π),sin(93π),sin(94π),−sin(93π),sin(92π),−sin(91π)⎦⎥⎥⎤
其中, KDST 就是 DST 的卷积核算子,但目前还是 浮点数的形式。浮点数矩阵不利于 GPU 算力的节省,因此还需要整数化。考虑 KDST 本身作用在实际像素取值上,而像素值的数据格式是以整数形式离散化存储的,具有位深数据范围中值记为常量 D 。
比如,8-bit 位深格式可取范围为 [0, 255] ,就有 D=128 取值。我们可以利用这一特点来对原数据进行放缩,并四舍五入取整。
记整数化后的 KDST 为 K^DST 则:
K^DST≈⎣⎢⎢⎡29748455,55,74,−29,−84,74,0,−74,74,84,−74,55,−29⎦⎥⎥⎤=D⋅KDST
原 DST 的算子,即可以转化为如下表示:
Xk(u,v)∣v=D1⋅D⋅KDST⋅Sp(x,y)=D1⋅K^DST⋅Sp(x,y)
当然,这里单独计算了分离后波矢 k⃗=(u,v) 对应平面波的权重 Xk(u,v) ,那么对于整个 4×4 区域所有的平面波权重(即傅立叶解)就有 等价矩阵 :
Xk∣4×4=(D1)2⋅K^DST⋅Sp∣4×4⋅K^DSTT
精简一下,即可写为:
Xk=(D1)2⋅K^DST⋅Sp⋅K^DSTT
这个即为 整数正弦变化(IDST)核心公式,而 K^DST 则被称为 整数正弦变化的基本算子(IDST Opt)。显然,在已知 Sp 和存储范围 D 的情况下,还是非常容易求得 Xk 的。而对应的 GPU 程序片也很简单,基本可当作滑动窗口移动步长 K=4 的固定算子乘法运算,就不再复写了。
整数离散正弦变换(IDST)的 GPU 矩阵算子
同理于 IDST,虽然 整数离散余弦变换(IDCT) 的切入理论,和 IDST 有一些不同。但最终的算子区别仅在于取值上。
仍然需要,将离散正弦变换扩展到二维情况。有:
DCT:Xk(u,v)k(u,v)&p(x,y)∈[(0, 0), (N−1, N−1)]εk∣k=(0,0)=√21&εk∣k≠(0,0)=1=(√2N2⋅εk)2⋅p=(0,0)∑(N−1,N−1)Sp(x,y)⋅cos(2N2x+1πu)⋅cos(2N2y+1πv)
依然,考虑可构成卷积核的子块最小大小为 4×4 ,则有 N=4 使上式变为:
DCT:Xk(u,v)k(u,v)&p(x,y)∈[(0, 0), (3, 3)]εk∣k=(0,0)=√21&εk∣k≠(0,0)=1=(√2εk)2⋅p=(0,0)∑(3,3)Sp(x,y)⋅cos(82x+1πu)⋅cos(2N2y+1πv)
如此,就可以矩阵表示 4×4 的 DCT 变化为:
DCT4×4:Xk(u,v)∣vεk∣k=(0,0)=KDCT⋅Sp(x,y)=[√2εv⋅y=0∑3(√2εu⋅x=0∑3cos(82x+1πu))⋅cos(82y+1πv)]⋅Sp(x,y)=√21⋅[εv⋅y=0∑3√21⋅(εu⋅x=0∑3cos(82x+1πu))⋅cos(82y+1πv)]⋅Sp(x,y)=√21&εk∣k≠(0,0)=1
即有:
KDCT=√21⎣⎢⎢⎢⎡√21cos(80π)cos(81π)cos(82π)cos(83π),√21cos(80π),cos(83π),cos(86π),cos(89π),√21cos(80π),cos(85π),cos(810π),cos(815π),√21cos(80π),cos(87π),cos(814π),cos(821π)⎦⎥⎥⎥⎤=√21⎣⎢⎢⎢⎡√21cos(81π)cos(82π)cos(83π),√21,cos(83π),−cos(82π),−cos(81π),√21,cos(83π),−cos(82π),cos(81π),√21,−cos(81π),cos(82π),−cos(83π)⎦⎥⎥⎥⎤
依然取位深数据范围中值记为常量 D 。有 D=128 对应 8-bit 位深格式 [0, 255] 的可取范围,使得我们能够将结果矩阵整数化处理。记整数化后的 KDCT 为 K^DCT 则:
K^DCT≈⎣⎢⎢⎡64836436,64,36,−64,−83,64,−36,−64,83,64,−83,64,−36⎦⎥⎥⎤=D⋅KDCT
原 DCT 的算子,即可以转化为如下表示:
Xk(u,v)∣v=D1⋅D⋅KDCT⋅Sp(x,y)=D1⋅K^DCT⋅Sp(x,y)
当然,这里单独计算了分离后波矢 k⃗=(u,v) 对应平面波的权重 Xk(u,v) ,那么对于整个 4×4 区域所有的平面波权重(即傅立叶解)就有 等价矩阵 :
Xk∣4×4=(D1)2⋅K^DCT⋅Sp∣4×4⋅K^DCTT
精简一下,即可写为:
Xk=(D1)2⋅K^DCT⋅Sp⋅K^DCTT
这个即为 整数余弦变化(IDCT)核心公式,而 K^DCT 则被称为 整数余弦变化的基本算子(IDCT Opt)。同样,在已知 Sp 和存储范围 D 的情况下,还是非常容易求得 Xk 的。而对应的 GPU 程序片也很简单,基本可当作滑动窗口移动步长 StepK=4 的固定算子乘法运算,就不再复写了。
现在汇总两者所述,对于整数离散正余弦变换(IDST/IDCT)的同理性,我们将 K^DST 与 K^DCT 统一称为 K^ 矩阵,即 整数离散正余弦变换算子(IDST/IDCT Opt)。而 K^ 的取值,显然和位深(Bit Depth)是强相关的。只有确定位深情况,才有固定的 K^ 矩阵。
因此,当存储格式(Data Format)位深为 8-bit 时目标 4×4 大小,整合后的公式如下 :
K^DST≈⎣⎢⎢⎡29748455,55,74,−29,−84,74,0,−74,74,84,−74,55,−29⎦⎥⎥⎤,Xk=(D1)2⋅K^DCT≈⎣⎢⎢⎡64836436,64,36,−64,−83,64,−36,−64,83,64,−83,64,−36⎦⎥⎥⎤K^⋅Sp⋅K^T
整合后的两种变化中, K^DCT 会将卷积核范围内大部分 低频信息 对应基底的 分离权重,富集到结果矩阵 Xk 的 左上角 ;而 K^DST 会将卷积核范围内大部分 低频信息 对应基底的 分离权重,富集到结果矩阵 Xk 的 右上角。而低频权重所对应的高残差区域,才是原始图像最关键的轮廓数据。因此,对于压缩场景,考虑到数据存储惯性,采用 K^DCT 得到关键权重值 Xk(0,0) 的方式更为合适。而 K^DST 则由于取用的基底函数类型,决定了其更适合平滑波动区域的数据处理,例如轮廓内的相对均匀填充部分。
我们通常将 K^DCT 得到的 Xk(0,0) 称为 直流系数(DC [Direct Coefficient]),而把 Xk 其余位置的基底函数权重值,称为 交流系数(AC [Alternating Coefficient)。
数据还原时,通过矩阵逆运算求得常量矩阵 K^−1 ,随后代入 Sp=D2⋅K^−1⋅Xk⋅K^−1T 式中还原原值。而对于其它类型的三角基底函数,和不同的目标窗口大小(常用为 2n , 取 n=2,3,4,5 ),使用基本公式代入,并按照上述推导类比处理,即可获取对应算子。
这就是最终主流的,整数离散正余弦变换。之于其它的 DST/DCT 共计 16 种类型,皆在特殊条件下起相关作用,被运用到针对子块的数据分离过程中。当然,推理过程依旧一致,只不过部分性质存在不同,如 DCT-8 就无法利用周期性来根据已知算子直接类推,每个不同的大小,都需要重新计算,这里不另作展开。
而对于整数离散正余弦变换本身来说,我们常用它来初步完成对子块内高低频数据的分离汇总,即对数据的分离归类。借此,方便后续在频域上,根据提纯结果进行压缩处理。对于其它位深取值,则根据 K^=D⋅K 计算即可,而 K 在窗口大小不变(即基底函数族固定)情况下,不会发生变化,可认为是一个常数矩阵。


