4.5.9 分类项-三元损失(Triplet Loss)
迭代公式:
图像:
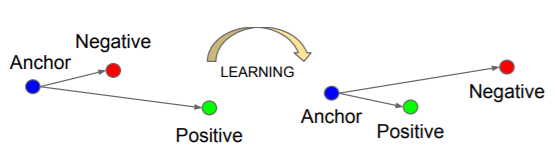
图 4-33 Triplet Loss 函数图[15]
特性:
- 使具有相同标签的样本(positive)之间的距离,尽量接近
- 使具有不同标签的样本(negative)之间的距离,尽量远离
- 要求输入 3 个分类样本子集:相似正样本集、相反负样本集、原样本对照集,并行训练
- 以 项代表被认为相似的确认半径,Loss 最小则理论上 Dn->m, Dp->0
- 越接近样本情况,损失越小
- 光滑(smooth),适合优化算法
- 非指数计算,算力消耗相对较低
三元损失(Triplet Loss) 函数来自于论文《FaceNet: A Unified Embedding for Face Recognition and Clustering》中 [15] ,提出的通过拆分 三元组(Triplet),选取正负样本与原样本进行差异化处理,来让预测值趋近于原样本而远离负样本的一种损失函数。
三元组(Triplet) 来自于输入分批的卷积神经网络(CNN)结果,我们需要将输入样本分为三类,在每一时代(Epoch)中都进行相同神经网络隐藏层权重(Wights)影响下的结果计算。累计 单次样本 的损失计算(Loss),以求得分批的损失函数(Cost Function)输出评分。
Triplet Loss 的使用
介于三元组损失提出最初目的,是为了进行人脸识别(FD [Face Detection]),我们因此取用人脸样本集举例。类似于人脸样本集,一般由 位不同人的 张该人不同脸的图片样本组成的,样本总量 大小的数据集。
以此为基础,三元组损失要求的三种样本分类子集分别是:
- 相似正样本集(Positives),由同人不同脸组成的 大小子集
- 相反负样本集(Negatives),由不同人不同脸组成的 大小子集
- 原样本对照集(Anchors),由不同人同脸(选一校订)组成的 大小子集
这三类子集,在数据分批后,会被分为相同批数并组合为一批数据,作为单次迭代输入数据,参与训练。我们仍然采用角标 来表示分批,那么有:
则,在分批数据参与一次批计算后,最终会构成 大小的一组 嵌入集(Embeddings),被我们用来计算损失函数(Loss)的实际处理对象。
最终,计算损失后的三元组,按照质量 来划分,可以分为三个类别:
- 易辨三元组(easy triplets),可以使得 loss 基本趋近于 0 的类型
- 难辩三元组(hard triplets),有 Dn < Dp 的三元组,一定会误判,尽量避免
- 模糊三元组(semi-hard triplets),有 Dp < Dn < Dp + m,这是我们重点训练的类型
可见,如果构成的三元组一上来就是易辨三元组,那只能证明模型训练参数的启动配置,使模型陷入了过拟合。通常,我们希望每一时代(Epoch)被计算的三元组都具有一定的模糊特性,而方便权重更新。因此,模糊三元组(semi-hard triplets)才是迭代的选择。
那么怎么评估当前的三元组,是否是模糊三元组呢?
其实很简单,通过当前正样本集所占有效样本的百分比,就能大致估算是否属于模糊类型。记正样本集百分比为 ,则有:
我们一般取 认为是一次有效训练中的模糊三元组数据。
三元损失在对比损失的基础上更近一步,引入了正负样本概念,来使得分类预测结果更加聚集,且使分类间能够更加远离。本身计算并不算非常复杂,因此可以用在如人脸识别、车辆识别等模型的移动端迁移上。但是,三元损失只是在对比损失上引入正负概念,实际处理过程中,每次只能对比一个负样本而忽略了其他的非关联性。这样就很容易造成迭代结果陷入不稳定(在多个距离相近但实际不同的负样本间抖动),或者局部最优解。
Triplet Loss 算子化
利用 C 语言实现对算子的封装,有:
#include <math.h>
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#define BATCH_SIZE 10 // Batch_size = Samples_of_Person x Data/Person
#define VECTOR_SIZE 128 // Extract output layer Feature vector's dimissions
#define DEVIDE_SAFE 1e-12 // protect when gridant at 0 will be to lage
// Pairwise Distance Calculation
void pairwise_distance(double embeddings[BATCH_SIZE][VECTOR_SIZE],
double distances[BATCH_SIZE][BATCH_SIZE], bool squared) {
for (int i = 0; i < BATCH_SIZE; i++) {
for (int j = 0; j < BATCH_SIZE; j++) {
double dot_product = 0.0;
double square_norm_i = 0.0;
double square_norm_j = 0.0;
for (int k = 0; k < VECTOR_SIZE; k++) {
dot_product += embeddings[i][k] * embeddings[j][k];
square_norm_i += embeddings[i][k] * embeddings[i][k];
square_norm_j += embeddings[j][k] * embeddings[j][k];
}
distances[i][j] = square_norm_i - (2.0 * dot_product) + square_norm_j;
if (!squared) {
if (distances[i][j] < 0.0) {
distances[i][j] = 0.0;
} else {
distances[i][j] = sqrt(distances[i][j]);
}
}
}
}
}
// Get Triplet Mask
void get_triplet_mask(int labels[BATCH_SIZE],
bool mask[BATCH_SIZE][BATCH_SIZE][BATCH_SIZE]) {
for (int i = 0; i < BATCH_SIZE; i++) {
for (int j = 0; j < BATCH_SIZE; j++) {
for (int k = 0; k < BATCH_SIZE; k++) {
// indices_equal
bool i_not_j = (i != j);
bool i_not_k = (i != k);
bool j_not_k = (j != k);
bool distinct_indices = (i_not_j && i_not_k && j_not_k);
// label_equal
bool i_equal_j = (labels[i] == labels[j]);
bool i_equal_k = (labels[i] == labels[k]);
bool valid_labels = (i_equal_j && !i_equal_k);
// mask depends on both
mask[i][j][k] = (distinct_indices && valid_labels);
}
}
}
}
// Batch All Triplet Loss
double triplet_loss(int labels[BATCH_SIZE],
double embeddings[BATCH_SIZE][VECTOR_SIZE], double margin,
bool squared, double *fraction_positives) {
// So, this only caused once per epoch for certain storage space
double pairwise_distances[BATCH_SIZE][BATCH_SIZE];
bool triplets_avail_masks[BATCH_SIZE][BATCH_SIZE][BATCH_SIZE];
// Pairwise distance calculation
pairwise_distance(embeddings, pairwise_distances, squared);
// Get triplet mask
get_triplet_mask(labels, triplets_avail_masks);
// Triplet loss calculation
int num_positive = 0;
int num_validate = 0;
double triplet_cost = 0.0;
{
for (int i = 0; i < BATCH_SIZE; i++) { // i for Anchor
for (int j = 0; j < BATCH_SIZE; j++) { // j for positive
for (int k = 0; k < BATCH_SIZE; k++) { // k for negative
double current_mask = triplets_avail_masks[i][j][k];
double current_loss =
fmax(0, current_mask * (pairwise_distances[i][j] -
pairwise_distances[i][k] + margin));
triplet_cost += current_loss;
// Calculate number of positive triplets and valid triplets
if (current_loss > 0) {
num_positive++;
}
if (current_mask > 0) {
num_validate++;
}
}
}
}
}
// Calculate fraction of positive triplets
*fraction_positives = (double)num_positive / ((double)num_validate + DEVIDE_SAFE);
return triplet_cost / (double)(num_positive + DEVIDE_SAFE);
}
int main() {
// Example input (fulfill to BATCH_SIZE x VECTOR_SIZE)
// Use Random labels and embeddings for testing
// Use three classes as different type, to generate labels
int type = 3;
int labels[BATCH_SIZE];
double embeddings[BATCH_SIZE][VECTOR_SIZE];
for (int i = 0; i < BATCH_SIZE; i++) {
labels[i] = rand() % type;
for (int j = 0; j < VECTOR_SIZE; j++) {
embeddings[i][j] = (double)rand() / (double)RAND_MAX;
}
}
double margin = 0.2;
double fraction_positives = 0.0;
double triplet_cost_value = triplet_loss(labels, embeddings, margin, false, &fraction_positives);
printf("The triplet loss is %f with positives %f \n", triplet_cost_value, fraction_positives);
return 0;
}
运行验证可得到结果:
The triplet loss is 0.270146 with positives 0.668605
虽然看上去比较复杂,然而在实际执行过程中, 一个时代(Epoch)只会执行一次三元组损失的计算,而空间复杂度上,仅额外增加了距离矩阵和遮罩的共 的空间大小。是完全可以接受的。
代码中,我们所使用的 遮罩(Mask)矩阵,实际上相当于将原论文中对三元组的三分类计算,用遮罩来代替了有效处理流程。这样做可行的基本原因,在于距离矩阵本身,在以整体分批不做区别输入的情况下,仍旧可以用全体分批包含样本的欧式距离,构成 大小的差异矩阵,记为 。以人脸检测为例,同人物同一张样本脸的情况,就相当于 的对角线位置。而对角线两侧的数据,则涵盖了同人不同脸、不同人的两种类型。
如此,计算所得 实际就包含和三元组的三分类计算中,不同分类的 所有距离类型。与此同时,最终损失函数的计算,是要叠加所有分类独立计算的单次损失的。进而,让我们有机会通过遮罩矩阵就能直接规划不同分类情况,应该取用哪一个距离值,来直接获取当次损失值叠加。如果记遮罩矩阵为 ,那么三元损失有工程公式:
而既然是矩阵乘法,除了本书例子中采用的纯 C 语言实现外,也可以通过 GPU 算子来实现进一步加速。类似于 CUDA 算子,或部分成熟的推理引擎(如 Keras、py-Touch 等)就是这样处理的。
从这个例子就能看出, 有效的工程化能够极大提升算法的训练效率,减小耗时。
这即是工程师在此处的关键作用。