4.5.3 回归项-休伯损失(Huber Loss)
迭代公式:
图像:
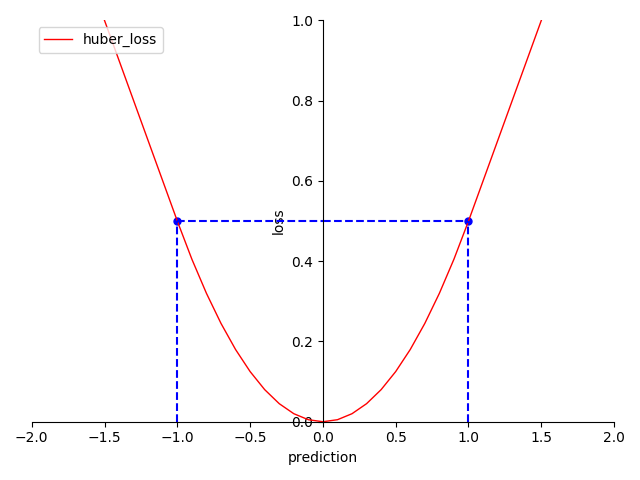
图 4-26 Huber Loss 函数图
特性:
- 当绝对误差在 时,契合正态分布(Normal distribution)
- 当绝对误差在 时,契合拉普拉斯分布(Laplace distribution)
- 当绝对误差小于 时,它采用平方误差,导数非常数
- 当绝对误差大于 时,采用的线性误差,导数常数 。
- 光滑(smooth),适合优化算法
- 非指数计算,算力消耗相对较低
休伯损失(Huber Loss) 实际上是基于 MAE 和 MSE 基础上,提出的一种兼容 MAE 与 MSE 各自优点的损失函数设计。
相比于 MSE 和 MAE,Huber Loss 的算力消耗没有太多的提升。相比于 MSE,Huber Loss 降低了 半径外对离群值的惩罚;相比于 MAE,Huber Loss 提高了 半径内回归的收敛速度。可以看出,Huber Loss 的效果首 的选择影响较大。因此,使用它的时候,需要注意 调参问题。
Huber Loss 算子化
利用 C 语言实现对算子的封装,有:
#include <math.h>
#include <stdio.h>
double huber_loss(double *y_true, double *y_pred, int size, double delta) {
double sum = 0;
for (int i = 0; i < size; i++) {
double error = y_true[i] - y_pred[i];
if (fabs(error) <= delta) {
sum += 0.5 * pow(error, 2);
} else {
sum += delta * (fabs(error) - 0.5 * delta);
}
}
return sum / size;
}
int main() {
int size = 3;
double y_true[] = {0.5, 0.75, 1.0};
double y_pred[] = {0.6, 0.8, 0.9};
double delta = 1.0;
double huber_loss_value = huber_loss(y_true, y_pred, size, delta);
printf("The Huber loss is %f\n", huber_loss_value);
return 0;
}
运行验证可得到结果:
The Huber loss is 0.033333