3.3.2 朴素目标检测结果度量 - IoU & GIoU

考虑到算法本身需要作为目标检测结果准确性的衡量标准，并用于模型的计算过程。所以不能采用较高复杂程度的算法。而 交并比（IoU [Intersection over Union]） 计算作为相对简单的区域检测算法，则是可被采用的不错方案。

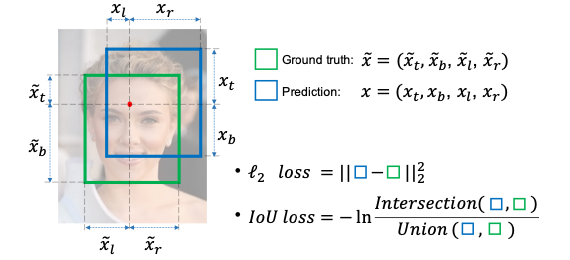
交并比顾名思义，即为交集和并集的比值。 只不过这里的交集和并集，指的是 预测结果（Prediction）对应的预测框（Anchor Box）和标注框（Ground Truth）的交集与并集，记为 I=IntersectionI = Intersection 和 U=UnionU = Union 。

图 3-11 原论文中交并比示意图[19]

如图所示，交并比公式非常简洁（注意 并非 IoU Loss ），可记为：

IoU=Intersection(Anchor, Truth)Union(Anchor, Truth)=IU {\displaystyle \begin{aligned} IoU &= \frac{Intersection(Anchor,\ Truth)}{Union(Anchor,\ Truth)} = \frac{I}{U} \\ \end{aligned} }

而根据交并比设计的损失函数，就是交并比损失函数（IoU Loss）。

同其他有关深度学习领域，针对损失函数提出的算法理论一致。IoU Loss 在模型中同样存在两项应用，分别为 前向预测（Forward Prediction） 和 反向传播（Backward Propagation）。 即标准损失的计算和模型梯度迭代的加速。

交并比损失函数（IoU Loss）

根据原论文的设计，IoU 前向扩散作用在 ReLU 激活函数层（ReLU Layer）后，以代替传统物体识别模型采用的 L2L_2 损失函数，判断待筛选的预测框是否命中。由于始终有 IoU∈[0, 1]IoU \in [0, \ 1] ，交并比损失函数可被认为是 p(IoU=1)=1p(IoU = 1) = 1 的 特殊交叉熵损失函数（cross-entropy Loss），有：

IoU Loss=−p⋅ln(IoU)−(1−p)⋅ln(1−IoU)∣p(IoU=1)=1=−ln(IoU) {\displaystyle \begin{aligned} IoU \ \mathcal{L}oss &= -p \cdot ln(IoU) - (1 - p) \cdot ln(1-IoU) | \quad p(IoU = 1) = 1 \\ &= -ln(IoU) \\ \end{aligned} }

带入交并比实际值，有：

IoU Loss=−lnIntersection(Anchor, Truth)Union(Anchor, Truth)=−lnIU {\displaystyle \begin{aligned} IoU \ \mathcal{L}oss &= -ln \frac{Intersection(Anchor,\ Truth)}{Union(Anchor,\ Truth)} = -ln \frac{I}{U} \\ \end{aligned} }

此即为 交并比损失函数。由于 IoU∈[0, 1]IoU \in [0, \ 1] 有 −ln(IoU)≈1−IoU-ln(IoU) \approx 1-IoU ，考虑到计算便利性，在条件范围内常用差值代替对数计算。即：

IoU Loss≈1−IoUIoU∈[0, 1] {\displaystyle \begin{aligned} IoU \ \mathcal{L}oss &\approx 1-IoU \quad IoU \in [0, \ 1] \\ \end{aligned} }

相比 L2L_2 损失函数的简单区域差值来衡量命中的方式， IoU 考虑到了 预测框与标准框的平面空间位置关系，并通过对位置的衡量 锁定了两者间的平面位姿独立优化，因而具有更贴合客观的代表性。且在交叉熵类型损失函数（详见下一章）的特性作用下，结果落于单位量化的百分比区间，利于阈值衡量和操作之便。

交并比损失函数（IoU Loss）的反向传播（Backward Propagation）

反向传播（Backward Propagation） 简单来说，是通过当前学习到的参数在参数空间内指定方向的运动趋势，来反相强化或衰减该方向上的参数权重，进而达到更快使模型拟合的数学方法论统称。自 杰弗里·辛顿（Geoffrey Hinton，“深度学习之父”，当代人工智能领域三巨头之一） 教授提出并汇总这一概念以来，持续的被作为深度学习根基理论之一，应用在各类算法的学习过程中。

如果从物理学角度来看，把参与训练的相关模型参数的权重向量比作速度，那么，损失函数的反向传播，就相当于 速度在各个方向上的某一时刻的加速度。所以，其影响的是权重在方向上的迭代步长变化，即为优化算法的输出。

交并比损失函数的反向传播，为便于称呼，简称 反向交并比（Backward IoU/ IoU Back）。取图 3.3.2-1 说明，记预测框为 x=(xl,xt,xr,xb)x = (x_l, x_t, x_r, x_b) 面积为 XX ，标注框为 x~=(x~l,x~t,x~r,x~b)\tilde{x} = (\tilde{x}_l, \tilde{x}_t, \tilde{x}_r, \tilde{x}_b) 面积为 X~\tilde{X} ，则反向交并比可表示为：

IoU Back=∂L∂x=I⋅(∇xX−∇xI)−U⋅∇xIU2⋅IoU=1U⋅∇xX − U+IUI⋅∇xI {\displaystyle \begin{aligned} IoU\ \mathcal{B}ack &= \frac{\partial \mathcal{L}}{\partial x} = \frac{I \cdot (\nabla_xX - \nabla_xI) - U \cdot \nabla_xI}{U^2 \cdot IoU} \\ &= \tfrac{1}{U} \cdot \nabla_xX \ - \ \tfrac{U+I}{UI} \cdot \nabla_xI \\ \end{aligned} }

其中， ∇xX\nabla_xX 是 预测框面积关于位置的偏导数（Partial Derivative）， ∇xI\nabla_xI 是 交集区域面积关于位置的偏导数，有：

Iw=min(xl, x~l)+min(xr, x~r)Ih=min(xt, x~t)+min(xb, x~b)∇xX={∂X∂xt(or ∂xb)=xl+xr∂X∂xl(or ∂xr)=xt+xb∇xI={∂I∂xt(or ∂xb)={Iw, if(xt<x~t or xb<x~b)0,otherwise∂I∂xl(or ∂xr)={Ih, if(xl<x~l or xr<x~r)0,otherwise {\displaystyle \begin{aligned} I_w &= min(x_l,\ \tilde{x}_l) + min(x_r,\ \tilde{x}_r) \\ I_h &= min(x_t,\ \tilde{x}_t) + min(x_b,\ \tilde{x}_b) \\ \nabla_xX &= { \begin{cases} \frac{\partial X}{\partial x_t( \mathbf{or}\ \partial x_b)} = x_l + x_r \\ \frac{\partial X}{\partial x_l( \mathbf{or}\ \partial x_r)} = x_t + x_b \end{cases} } \\ \nabla_xI &= { \begin{cases} \frac{\partial I}{\partial x_t( \mathbf{or}\ \partial x_b)} = { \begin{cases} I_w &, \ if ( x_t < \tilde{x}_t\ \mathbf{or}\ x_b < \tilde{x}_b ) \\ 0 &, otherwise \end{cases} } \\ \frac{\partial I}{\partial x_l( \mathbf{or}\ \partial x_r)} = { \begin{cases} I_h &, \ if ( x_l < \tilde{x}_l\ \mathbf{or}\ x_r < \tilde{x}_r ) \\ 0 &, otherwise \end{cases} } \end{cases} } \\ \end{aligned} }

带入求得 IoU BackIoU\ \mathcal{B}ack 值，作用于 优化算法的梯度变换，如 自适应动量算法（Adam） 等。来发挥相应作用。

交并比损失函数（IoU Loss）的简单 C++ 语言实现

到这里，我们就可以根据基本情况来做一下交并比的代码实现了。由于需要进行一些基本的矩阵运算，我们选择采用引入 轻量级的 GLM（GL Mathematics） 开源库，来协助完成基本工作。

我们选择 GLM 库的原因，是因为其可以通过纯粹的包含头文件的方式，简便轻巧的启动包含基本图形矩阵数据结构和方法的完整库功能。在其开源协议保证下，非常适合运用于大部分工程项目。如果需要也可以自己分装部分算法和操作。例如在某些场景下，我们需要计算物体体积方块区域，到视窗平面上的投影位置：

#include <glm/ext.hpp>

#include "stdio.h"
#include "math.h"

typedef glm::vec2 Vector_2f;
typedef glm::vec3 Vector_3f;
typedef glm::vec4 Vector_4f;
typedef glm::mat2 Matrix_2x2f;
typedef glm::mat3 Matrix_3x3f;
typedef glm::mat4 Matrix_4x4f;

#define XC_PI 3.14159265358979323846
#define XC_RADIAN(d_) (XC_PI * d_ / 180.0f)
#define XC_VECTOR_NORMALIZE(v_) glm::normalize(v_)
#define XC_VECTOR_CROSS(vl_, vr_) glm::cross(vl_, vr_)
#define XC_VECTOR_DOT(vl_, vr_) glm::dot(vl_, vr_)
#define XC_MATRIX_INVERSE(m_) glm::inverse(m_)
#define XC_MATRIX_TRANSPOSE(m_) glm::transpose(m_)
#define XC_MATRIX_DOT(ml_, mr_) dot_m4x4(ml_, mr_)
#define XC_V4_M44_DOT(vl_, mr_) dot_v4_m4x4(vl_, mr_)

Vector_4f
dot_v4_m4x4(Vector_4f v4_, Matrix_4x4f m4x4_) {
    return m4x4_[0] * v4_[0] + m4x4_[1] * v4_[1] + m4x4_[2] * v4_[2] + m4x4_[3] * v4_[3];
}

Matrix_4x4f
dot_m4x4(Matrix_4x4f ml_, Matrix_4x4f mr_) {
    Matrix_4x4f result_;
    result_[0] = mr_[0] * ml_[0][0] + mr_[1] * ml_[0][1] + mr_[2] * ml_[0][2] + mr_[3] * ml_[0][3];
    result_[1] = mr_[0] * ml_[1][0] + mr_[1] * ml_[1][1] + mr_[2] * ml_[1][2] + mr_[3] * ml_[1][3];
    result_[2] = mr_[0] * ml_[2][0] + mr_[1] * ml_[2][1] + mr_[2] * ml_[2][2] + mr_[3] * ml_[2][3];
    result_[3] = mr_[0] * ml_[3][0] + mr_[1] * ml_[3][1] + mr_[2] * ml_[3][2] + mr_[3] * ml_[3][3];
    return result_;
}

此处我们简单的实现了两个快速算法，用于协助我们完成目标 4×14 \times 1 向量与 4×44 \times 4 矩阵的点乘，和两个 4×44 \times 4 矩阵的点乘。 其实类似的快速算法已在库内有封装，此处仅是用于说明 GLM 的一些基本用法。

不过，对于交并比的代码工程化来说，并不需要这么复杂：

#include <glm/ext.hpp>

#include "stdio.h"
#include "math.h"

typedef glm::vec2 Vector_2f;
typedef glm::vec4 Vector_4f;

bool static IoU_simple(Vector_4f anchor_box_, Vector_4f ground_box_, float threshold_ = 0.8f) {
    float M_area_, T_area_, I_area_, U_area_;
    float IoU_mark_;
    {
        Vector_2f I_lt = {
            MAX(anchor_box_[0], ground_box_[0]),
            MAX(anchor_box_[1], ground_box_[1])
        };
        Vector_2f I_rb = {
            MIN(anchor_box_[2], ground_box_[2]),
            MIN(anchor_box_[3], ground_box_[3])
        };
        if (I_rb.x < I_lt.x || I_rb.y < I_lt.y) {
            return false;
        }
        M_area_ = MAX(ABS(anchor_box_[2] - anchor_box_[0]), 0) *
                  MAX(ABS(anchor_box_[3] - anchor_box_[1]), 0);
        T_area_ = MAX(ABS(ground_box_[2] - ground_box_[0]), 0) *
                  MAX(ABS(ground_box_[3] - ground_box_[1]), 0);
        I_area_ = MAX(ABS(I_lt.x - I_rb.x), 0) * MAX(ABS(I_lt.y - I_rb.y), 0);
        U_area_ = M_area_ + T_area_ - I_area_;
        IoU_mark_ = I_area_ / U_area_;
    }
    return (1 - IoU_mark_ > threshold_);
}

上面的简短过程，就是整个交并比的 C++ 语言封装了。可见易于迁移。

IoU 的缺点与 GIoU 的改进

交并比损失函数并非是没有缺陷的。 一个显而易见的问题就是 IoU 无法评估预测框和标注框无交集区域时，预测框的优劣程度（梯度消失）。 这所造成的直接问题就是，当 无交集情况出现，我们将无法只通过 IoU 损失函数，来使预测框快速的向标注框方向运动。从而导致数据浪费并产生不准确的结果，且有可能使模型陷入局部解而导致停滞。

2019 年的 CVPR 上，来自斯坦福大学的研究团队以交并比为基础，提出了 IoU 的改进版 通用交并比（GIoU [Generalized Intersection over Union]）算法 [20] 。解决了无交集的判断问题。

GIoU 采用的处理办法为，在原有 IoU 计算的基础上，引入预测框与标注框区域所构成的最小外接矩形，即 两者的最小外接闭包（smallest enclosing convex） 参与损失函数计算，来辅助量化两者之间的远近到权重迭代中， 记为 C=ConvexC = Convex 。

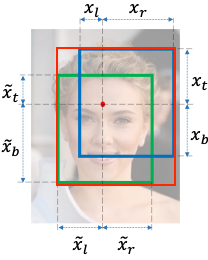
图 3-12 红框即为 IoU 图例中，I 和 U 的最小外接矩形

改进后的通用交并比公式 同样非常简洁 （注意 并非 GIoU Loss ），可记为：

GIoU=IoU−∣C−(A∪B)∣∣C∣=IoU−∣C−U∣∣C∣ {\displaystyle \begin{aligned} GIoU &= IoU - \frac{|C - (A \cup B)|}{|C|} = IoU - \frac{|C - U|}{|C|} \\ \end{aligned} }

从公式可知，当 预测框与标注框不存在交集时， U=∣A∪B∣=0→IoU=0U = |A \cup B| = 0 \rightarrow IoU = 0 有：

GIoU=IoU−C−0C=−1 {\displaystyle \begin{aligned} GIoU &= IoU - \frac{C-0}{C} = -1 \\ \end{aligned} }

当 预测框与标注框完全重合时， I=∣A∩B∣=∣A∪B∣=U→IoU=1I = |A \cap B| = |A \cup B| = U \rightarrow IoU = 1 有：

GIoU=IoU−C−UC=IoU−0C=1 {\displaystyle \begin{aligned} GIoU &= IoU - \frac{C-U}{C} = IoU - \frac{0}{C} = 1 \\ \end{aligned} }

基于此，GIoU 的取值范围为 GIoU∈[−1, +1]GIoU \in [-1, \ +1] 。

通用交并比损失函数（GIoU Loss）

GIoU 本质是一种对 IoU 算法的 泛化补充，所以在损失函数 GIoU LossGIoU \ \mathcal{L}oss 的表达上，直接采用 GIoU 代替 IoU 作为影响因子即可。有：

GIoU Loss=−ln(GIoU)≈1−GIoUGIoU∈[−1, 1] {\displaystyle \begin{aligned} GIoU \ \mathcal{L}oss & = -ln(GIoU) \approx 1-GIoU \quad GIoU \in [-1, \ 1] \\ \end{aligned} }

同理，记 ∇xX\nabla_xX 是预测框面积关于位置的偏导数（Partial Derivative）， ∇xX~\nabla_x\tilde{X} 是标注框面积关于位置的偏导数（Partial Derivative）， ∇xI\nabla_xI 是交集区域面积关于位置的偏导数，有：

GIoU Back=∂L∂x=∂LIoU∂x+∂LUoC∂x=I⋅(∇xX−∇xI)−U⋅∇xIU2⋅IoU+U⋅(∇xX+∇xX~)−C⋅(∇xX−∇xI)C⋅U=1U⋅∇xX − U+IUI⋅∇xI + 1U⋅∇xI +1C⋅∇xX~ − C−UCU⋅∇xX=1C⋅∇xX − 1I⋅∇xI + 1C⋅∇xX~ {\displaystyle \begin{aligned} GIoU\ \mathcal{B}ack &= \frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}_{IoU}}{\partial x} + \frac{\partial \mathcal{L}_{UoC}}{\partial x} \\ &= \frac{I \cdot (\nabla_xX - \nabla_xI) - U \cdot \nabla_xI}{U^2 \cdot IoU} + \frac{U \cdot (\nabla_xX + \nabla_x\tilde{X}) - C \cdot (\nabla_xX - \nabla_xI)}{C \cdot U} \\ &= \tfrac{1}{U} \cdot \nabla_xX \ - \ \tfrac{U+I}{UI} \cdot \nabla_xI \ + \ \tfrac{1}{U} \cdot \nabla_xI \ + \tfrac{1}{C} \cdot \nabla_x\tilde{X} \ - \ \tfrac{C-U}{CU} \cdot \nabla_xX \\ &= \tfrac{1}{C} \cdot \nabla_xX \ - \ \tfrac{1}{I} \cdot \nabla_xI \ + \ \tfrac{1}{C} \cdot \nabla_x\tilde{X} \\ \end{aligned} }

而 标注框在单次迭代中是常量值，即 ∇xX~=0\nabla_x\tilde{X} = 0 代入：

GIoU Back=1C⋅∇xX − 1I⋅∇xI {\displaystyle \begin{aligned} GIoU\ \mathcal{B}ack &= \tfrac{1}{C} \cdot \nabla_xX \ - \ \tfrac{1}{I} \cdot \nabla_xI \end{aligned} }

显然 GIoU 的反向传播计算相比 IoU 更为快捷有效。这也是其 通用性 的体现之一。

通用交并比损失函数（GIoU Loss）的简单 C++ 语言实现

万事具备，现在只需要代码实现 GIoU 算法即可，仍然非常便捷。只需在原 IoU 算法上补充改进部分即可：

#include <glm/ext.hpp>

#include "stdio.h"
#include "math.h"

typedef glm::vec2 Vector_2f;
typedef glm::vec4 Vector_4f;

bool static GIoU_simple(Vector_4f anchor_box_, Vector_4f ground_box_, float threshold_ = 0.8f) {
    float M_area_, T_area_, I_area_, U_area_, C_area_;
    float IoU_mark_, GIoU_mark_;
    {
        Vector_2f I_lt = {
            MAX(anchor_box_[0], ground_box_[0]),
            MAX(anchor_box_[1], ground_box_[1])
        };
        Vector_2f I_rb = {
            MIN(anchor_box_[2], ground_box_[2]),
            MIN(anchor_box_[3], ground_box_[3])
        };
        if (I_rb.x < I_lt.x || I_rb.y < I_lt.y) {
            return false;
        }
        M_area_ = MAX(ABS(anchor_box_[2] - anchor_box_[0]), 0) *
                  MAX(ABS(anchor_box_[3] - anchor_box_[1]), 0);
        T_area_ = MAX(ABS(ground_box_[2] - ground_box_[0]), 0) *
                  MAX(ABS(ground_box_[3] - ground_box_[1]), 0);
        I_area_ = MAX(ABS(I_lt.x - I_rb.x), 0) * MAX(ABS(I_lt.y - I_rb.y), 0);
        U_area_ = M_area_ + T_area_ - I_area_;
        IoU_mark_ = I_area_ / U_area_;
    }
    {
        Vector_2f C_lt = {
            MIN(anchor_box_[0], ground_box_[0]),
            MIN(anchor_box_[1], ground_box_[1])
        };
        Vector_2f C_rb = {
            MAX(anchor_box_[2], ground_box_[2]),
            MAX(anchor_box_[3], ground_box_[3])
        };
        if (C_rb.x < C_lt.x || C_rb.y < C_lt.y) {
            return false;
        }
        C_area_ = MAX(ABS(C_lt.x - C_rb.x), 0) * MAX(ABS(C_lt.y - C_rb.y), 0);
        GIoU_mark_ = IoU_mark_ - (C_area_ - U_area_) / C_area_;
    }
    return ((1.0 - GIoU_mark_) * 0.5f > threshold_);
}

完成 GIoU 算法的程序化封装。

GIoU 的缺点与 IoU 算法族的发展

那么，GIoU 算法是否依旧存在缺陷呢？

虽然 GIoU 可以适度的缓解无交集情况的梯度消失问题，但 并不能加速当预测框完整包含标注框时的梯度迭代。此时 GIoU 算法，会因为最小外接矩形等同于并集 的缘故，退化为 IoU 算法。从而无法起到有向加速梯度趋向更贴合标注大小的目的。

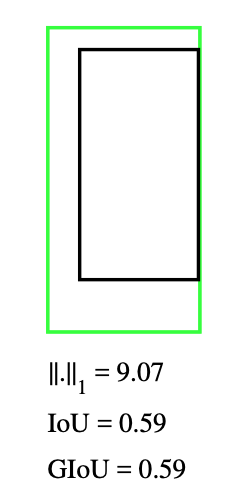
图 3-13 预测框（绿）包含标注框时 GIoU 退化为 IoU 示意图[20]

针对这种情形，后续的一些研究试图通过引入 框中心点（DIoU [Distance-IoU]） [21] ，结合 长宽一致性（CIoU [Complete-IoU]） [21] ，并在中心点基础上 进一步优化损失函数的设计（EIoU [Efficient-IoU]） [22] 来解决此问题。虽然取得了不错的效果，但算法复杂度也有较大变化，考虑到实际工程情况取舍可以酌情选用，本书不再展开讲解。

几种算法的对比结果如表 《当前主流 IoU 算法族基于 COCO val-2017 数据集的对比结果》 所示 [22]，仅供参考：

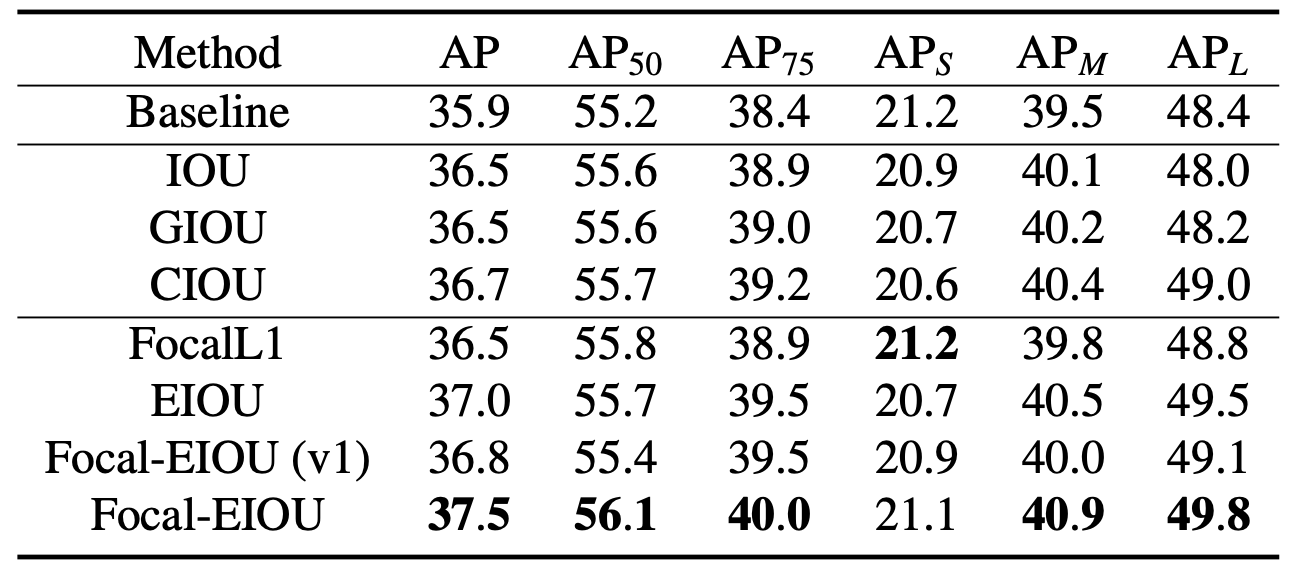
进行到这里，在一些耗时训练之后，我们就能够得到一个静态的物体识别算法模型了。 由于静态模型不需要持续迭代，通过直接取模型参数或者接入其他成型的推理引擎，即可完成对指定关注物体的识别操作。

需要注意的是，目前训练所得的 简易模型，还不能在 不经过辅助方法 的情况下，自主完成锁定需要检测的物体。模型只能用于判断某一个给定检测范围（检测框）内的数据，是否属于被用于训练录入的标签物体，并给出命中率。

因此，依旧需要人为提供用于辅助锁定检测目标的方法。 配合检测所得命中率经过阈值筛选最终结果，得到其所处像素位置。

Copyright © Since 2021 李述博 (Arikan.Li) , All Rights Reserved all right reserved，powered by GitbookLast Updated: 2024-09-12 12:11:10

results matching ""

    No results matching ""