4.5.6 分类项-交叉熵损失(Cross Entropy Loss)
迭代公式:
图像:
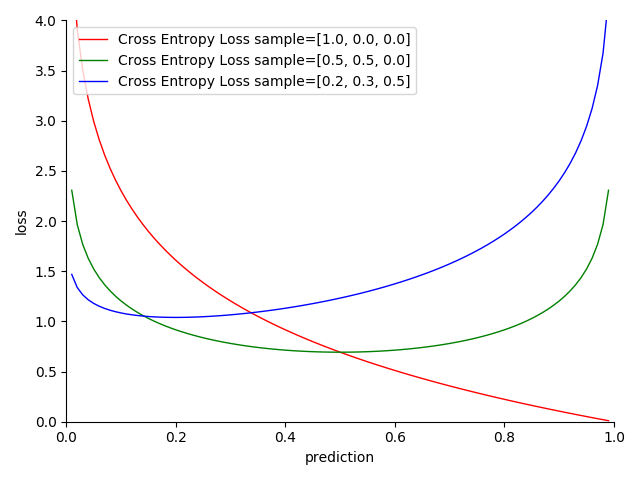
图 4-30 Cross Entropy Loss 函数图
特性:
- 契合逻辑分布(Logistic distribution)样本,拟合 Softmax 模型
- 二分类下的交叉熵损失表现,二者本质等价
- 越接近目标,损失越小
- 越趋近两极,结果越准确
- 基于贝叶斯统计(Bayesian statistics),采用交叉熵估计
- 光滑(smooth),适合优化算法
- 对数计算,算力消耗相对较高
交叉熵损失(CEL [Cross Entropy Loss]) 是一种处理分布于高维同平面(K-Space)下独热向量(one-hot vector)样本集的聚类分析手段。交叉熵损失函数是一种为了 配合 Softmax 激活函数 的损失函数设计,输出满足概率累和为 1。这是因为交叉熵的本质,是试图用预测值来表示某个事件发生所需要的平均概率,从概念上,将事物可能发生的几率,和事物不可能发生的几率做了二元分割,即 Log Loss 实际上是 CEL 的最简表示形式。
所以,在使用交叉熵损失前,最好 先对参与交叉熵运算的所有同样本,进行一次 Softmax 处理,以求尽可能保证估计值之和为 1。
但是需要注意的是,交叉熵损失本身,并不依赖于是否对输入概率进行了归一化。也就是说,虽然可以进行估值之和大于 1 的输入处理,但本身会相对失去意义。因为,CEL 的结果越小,越说明分类估值准确性。非归一化输入只会干扰结果,从而影响模型准确。
Cross Entropy Loss 算子化
利用 C 语言实现对算子的封装,有:
#include <math.h>
#include <stdio.h>
double cross_entropy_loss(double *y_true, double *y_pred, int size, int num_classes) {
double sum = 0;
for (int i = 0; i < size; i++) {
for (int j = 0; j < num_classes; j++) {
sum += y_true[i * num_classes + j] * log(y_pred[i * num_classes + j]);
}
}
return -sum / size;
}
int main() {
int size = 3;
double y_true[] = {0.5, 0.75, 1.0}; // single sample base 'cat' 'puppy' 'dog'
double y_pred[] = {0.6, 0.8, 0.9}; // single sample pred 'cat' 'puppy' 'dog'
int num_classes = 3;
double loss_value = cross_entropy_loss(y_true, y_pred, size, num_classes);
printf("The cross entropy loss is %f, for 'cat' 'puppy' 'dog' ", loss_value);
return 0;
}
运行验证可得到结果:
The cross entropy loss is 0.1982671, for 'cat' 'puppy' 'dog'
上面的代码中,展示了存在三类分类情况下,样本的输入分类和预测特征向量,皆未归一化会产生的结果。交叉熵损失仍然能使用,但不精确。