1.4.2 乐理:和声(Harmony) & 和弦(Chord)& 调性网络(Tonnetz)
我们对乐理音调到感观转换已有基本认知。但当我们遇到一些频率不在表中,且也不属于表中任意一个独立音调频率倍数(即其它音级),却又悦耳到想要记录的,非隶属单一琴键的声音时。或者想要合理的创造一种不存在于自然中的合成音时。音调频率比关系的平滑听感,就成为了指引。
它使我们可以通过已有音调频率的合理组合,以响度代替融合比例(可以说是古早的混音了,非常感性比较考验演奏者水平),来拟合新的声音。
在乐理中,称之为 和声(Harmony)。
和声(Harmony) & 协和(Consonance)& 不协(Dissonance)
和声(Harmony) 是指将音调以两两形式组和,而产生新的声音的过程。当然,为了给予艺术发挥空间,不会也不能固定响度入内。所以,和声是指参与声音其音色频率链的合成。此处为了通用说明,需要固定图形化时,采用相同大小的抽象响度表示。
不过请注意,在实际在数字合成过程中,还是需要 结合响度构建和声后的新谐波链的。

图 1-13 某钢琴同音级下纯一度(P1)与纯五度(P5)的泛音链和声图
上例为同音级的 P1 + P5 和声(如 C4 + G4)。这样的一组声音同时弹奏时,为人们带来了听感上的和谐。而同音级下的 P1 + M2 和声(如 C4 + D4),则没有这么融洽:

图 1-14 某钢琴同音级下纯一度(P1)与大二度(M2)的泛音链和声图
从两者和更多样本的 频率链重叠情况上,过往的研究者们发现,如果参与合成的声音,在频率链上有 较多的重合谐波 时,人耳会觉得声音 和谐(Harmony) 不突兀。
而同音名不同级的 乐理音调(Musical Note),其 谐波链几乎完全重合,各频率总是相差 2 的整数倍大小。如 C4 + C5 或 F4 + F6 等,几乎可以认为就是一个声音。依此称为 完美协和(Perfect Consonance)。
但相仿 P1 + P5 和声情况的音调组合,其 谐波链存在较多重合,却依然可以被分辨。我们称其为 不完美协和(Inperfect Consonance)。
而相仿 P1 + M2 和声情况的音调组合,其 谐波链几乎很少重合,参与基音相对可辨。我们称之为 不协(Dissonance)。
至于不协情况中,其 谐波链在一定范围内完全无重合的情况,参与基音完全可辨。我们称之为 完全不协(Perfect Dissonance)。
同理,可以扩展至更复杂的和声组合。
显然,协与不协的问题,同人耳对频率的敏感度高度相关。
仍然采用该音级 4 的例子。以 12 个音调间和声情况统计。距离 C4 基础音调的音程(Interval)和 大致频率比(C4: 当前音调,精确小数点后一位)如下:
| C4 | C♯ D♭ |
D | D♯ E♭ |
E | F | F♯ G♭ |
G | G♯ A♭ |
A | A♯ B♭ |
B | C5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | m2 | M2 | m3 | M3 | P4 | A4/d5 | P5 | m6 | M6 | m7 | M7 | P8 |
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
| 1:1 | 16:15 | 9:8 | 6:5 | 5:4 | 4:3 | 45:32 | 3:2 | 8:5 | 5:3 | 16:9 | 15:8 | 2:1 |
表中,橙色 表示与 C4 完美协和,黄色 表示与 C4 不完美协和,蓝色 表示与 C4 不协,靛色 表示与 C4 完全不协。将统计扩展到整个当前音级中两两音调时,就有(音程 P1 省略比例):
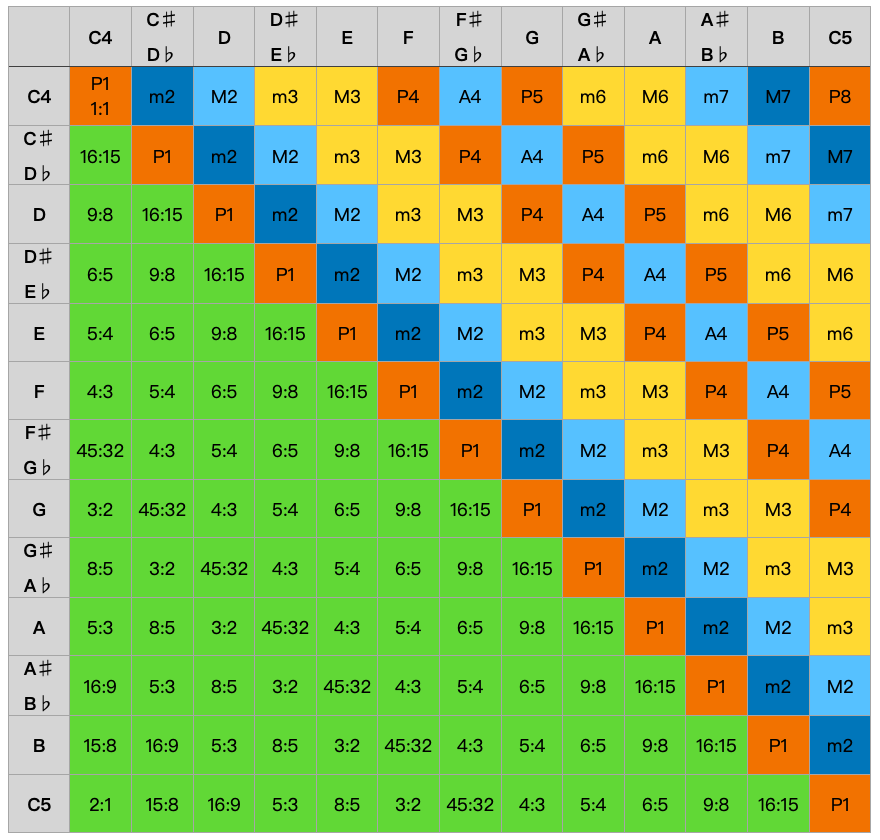
可见,
- 当两音调间音程 为 时,两音调和声 完美协和 ;
- 当两音调间音程 为 时,两音调和声 不完美协和 ;
- 当两音调间音程 为 时,两音调和声 不协 ;
- 当两音调间音程 为 时,两音调和声 完全不协 ;
至此,我们便可以利用此规律,使构成复杂和谐音的组成音,满足两两和声协和匹配。继而创造出新的声音。
这种特殊的和声过程,即是和弦(Chord)。
和弦(Chord)& 三和弦(Triad)
以协和(包括完美协和、不完美协和)音程规律,取一组由升调方向选择的三个或更多音调组成的和声,在乐理中被称为 和弦(Chord)。 和弦以成组的两两相邻音间音程差异,分 三度和弦 和 非三度和弦 两个类别。
三度弦,即以三度音程(包括 m3、M3)构成的一组和弦。 根据组成的个数又可以细化为:三和弦(三音) 、 七和弦(四音) 、 九和弦(五音) 、 十一和弦(六音) 、 十三和弦(七音)。
非三度弦,即音间音程非三度。 情况则较为复杂,包括 转位/离调和弦 所代表的一系列和弦。
在工程上,相对较常用的是三度弦。而三度弦分类下,各中和弦概念存在基本规律,可以直接从三和弦向上衍生。因此,为了便于记忆,本书采用三和弦(三音)讲解。至于非三度弦的其它类型,借助对三和弦的理解,需要时再行查阅乐理专业资料即可。
三和弦(Triad) 的组成音有三个,根据 升调 顺序被分别称为 一音(First) 、 三音(Third) 、 五音(Fifth)。有时也称为 根音(R [Root]) 、 中音(M [Mediant]) 、 冠音(T [Top])。
- 根音(R),即一音(First),指组成音中位于低音位置的音调;
- 中音(M),即三音(Third),指组成音中与根音音程三度的音调;
- 冠音(T),即五音(Fifth),指组成音中与根音音程五度的音调; 一般的,我们会结合两种称谓,用 根音(Root) 、 三音(Third) 、 五音(Fifth) 指代三和弦组成。
因为三度、五度包含了共有 m3、M3、d5、P5、A5 的 5 种音程在内的类型。在根音选定时,可以产生 4 种不同的组合方式,有:
- 大三和弦,取 Root + M3 + P5,记为 ;
- 小三和弦,取 Root + m3 + P5,记为 ;
- 增三和弦,取 Root + M3 + A5,记为 ;
- 减三和弦,取 Root + m3 + d5,记为 ;
根音的选择是不受限的,比如取 C4 即 C大调的主音为根音,则有 C4 下的 大/小/增/减三和弦分别为:
而取 C大调 的 F4 为根音,则有 F4 下的 大/小/增/减三和弦分别为:
这种组合类型是固定的,可以类推至任意音调。理论适用于所有三度音程和弦,即三度弦。
不过,因为音程之于 自然音阶 间的转换原因。通过组合公式,直接计算的方式依旧会显得比较繁琐。能不能参考五度圈对大/小调的查表方式,构建一个相类似的查表法,来快速完成多音调的和弦组合呢?
答案是可以的,调性网络(Tonnetz) 就是答案。
调性网络(Tonnetz)
现代调性网络(Tonnetz)原型,来自于数学大家 莱昂哈德·欧拉(Leonhard Euler,1707~1783) 在早年尝试的,以数学建模构造良好合声的探索 [10] 。欧拉首次采用数学图论方法,解决和弦问题,提出了 欧拉调性网络(Euler's Tonnetz,Tonnetz 是德语,相当于英文的 Tone-net)。
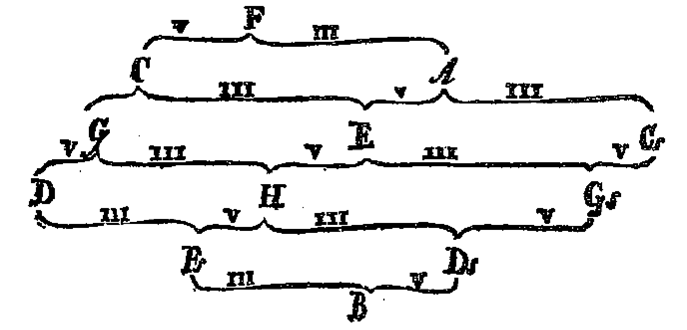
图 1-15 欧拉论文原稿中的调性网络(Euler's Tonnetz)示意图
欧拉调性网络可视化的表示了,协和和弦间的音程关系。从上而下的标识了两种联系。位于 上方的音调,其 左分支 是距离它最近的五度(P5、d5、A5)音程对应音调,而 右分支 是距离它最近的大三度(M3)音程对应音调。例如,F->C(F4->C5) 有 C 是 F 的 P5,F->A(F4->A4) 有 A 是 F 的 M3。全图涵盖了同音级下的一套完整标准十二律。
不过因为范围和和弦上的局限性,欧拉调性网络没有得到太多的应用。
状态一直持续到 19 世纪时期末,被 胡戈·里曼(Hugo Riemann,1849~1919) 打破。
胡戈·里曼结合五度圈查表法有关升降调的螺旋延展性,在对 大小调间和弦二元性(Major/Minor Chord Dualism) 的研究时,发现了大三和弦和小三和弦间,在欧拉调性网络沿音级的五度展开上。可以通过简单的 平移变换(Schritt) 和 倒影变换(Wechsel),得到同源与相邻向上/向下和弦效果。由此,提出了 里曼理论(Riemannian Theory)。并在这之后,将原有两个主要变换中的倒影变换,扩展到了 关系变换 与 导音变换 双变换。结合原有大小和弦二元论的 平移变换,构成三主要变换体系 [11] ,称为 新里曼三元理论(Neo-Riemannian Triadic Theory),简称 新里曼理论(Neo-Riemannian Theory)。
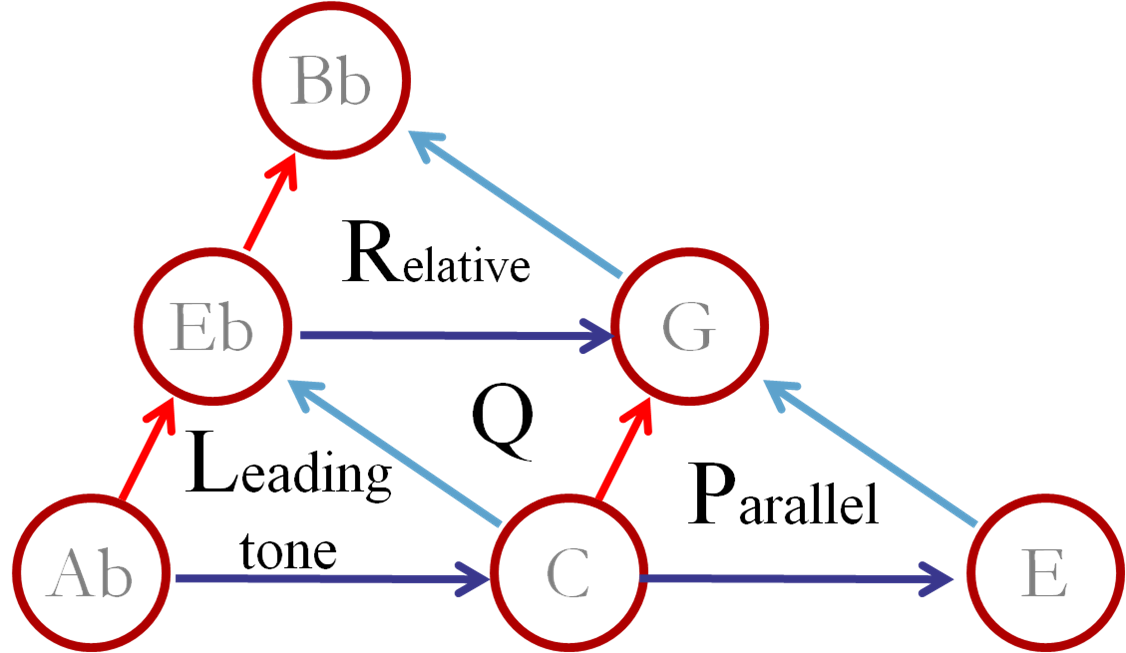
图 1-16 新里曼理论(Neo-Riemannian Theory)的三主要变换
注意,上图中选择三和弦时,必须按照从根音到冠音的相同箭头方向选择。箭头表示了 位于下一位 的组成音。
依托调性网络的几何化,新里曼理论的 三种主要变换,分别是:
P变换(P Transformation),即 平行变换(Parallel Transformation)。如上图蓝色箭头标识关键步骤。 P变换只能在完全相同主音的自然音阶,即同一大/小调,内进行。
在已知一则三和弦组成情况下,查询根音(Root)和五音(Fifth)相同的另一组三和弦的方式。再以根音五音连线作为平行四边形对角线,用两组三音(Third)构造平行四边形。、结果中与原三和弦中音相对的另一角,为所求和弦中音。如图中 。
P变换,让我们能够快速完成 同主音间 大/小三和弦 的转换。
R变换(R Transformation),即 关系变换(Relative Transformation)。如上图红色箭头标识关键步骤。 R变换只能在主音音程互为小三度(m3)关系的自然音阶,即关系调(Relative Key),间进行。
在已知一则三和弦组成情况下,通过将五音(Fifth)升/降一个五度(P5、d5、A5),再次以移动后的五音(Fifth)与原三和弦三音(Third)查询 大/小调的同位关系三和弦。构成结果平行四边形的另一角,就是升调方向时所求关系大调五音,或降调方向时所求关系小调根音。如图中 。
R变换,让我们能够快速完成 关系调间 大三和弦 与 小三和弦 的转换。
L变换(L Transformation),即 导音变换(Leading-Tone Transformation)。如上图靛色箭头标识关键步骤。 L变换只能在主音音程互为升调方向纯五度(P5)关系的自然音阶,即相邻调(Adjacent Key),间进行。
在已知一则三和弦组成情况下,通过将五音(Fifth)升/降一个大三度(M3),查询新位置下的五音所处的三和弦。构成结果平行四边形的另一角,就是升调方向时所求相邻调五音,或降调方向时所求相邻调根音。如图中 。
L变换,让我们能够快速完成 相邻调间 大/小三和弦 的转换。
新里曼理论,进一步完善了现代调性网络的音程变换图系统。使得以该理论为根据的几何建模,存在 无限延伸的音调覆盖 和 快速可查 的特点。从而变得足够泛化且实用。由此绘制而成的新里曼理论平面拓扑调性网络,成为了三和弦的快速查表法的基石:
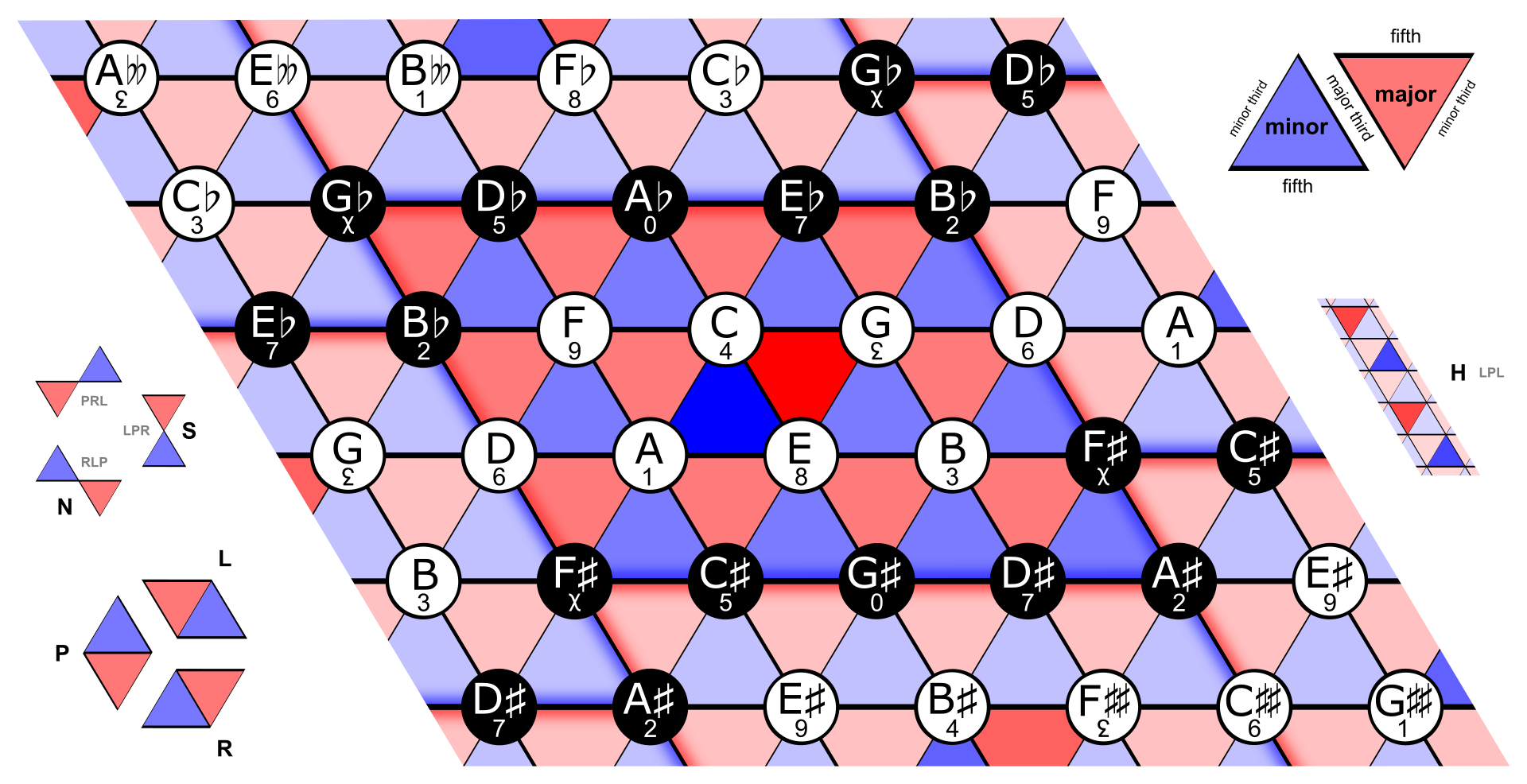
图 1-17 以新里曼理论(Neo-Riemannian Theory)绘制的调性网络
再配合上五度圈的自然音阶快速确定,与音序频率表的音调频率映射关系,即可完成对和弦的音调频率转换。 以频率,打通乐理到心理声学、声乐工程的关系。
至此,我们已经掌握了基础的乐理观测方法,并能够较为客观的评判。而在前文中,我们提到人耳对频率的感知,是促成一切的关键。而心理声学的实验结果,是其客观数据化的前提。 那么,其具体是怎样的测量过程,而结果又是怎样体现的呢?
这就需要提到 等响曲线(Equal Loudness Level Contour) 了。