4.3 经典激活函数(Classic Activation Function)
激活函数(Activation Function) 是一种被设计用来,在模型训练的每个单元数据输入位置,为输入引入非对称性特征 的特殊辅助函数。
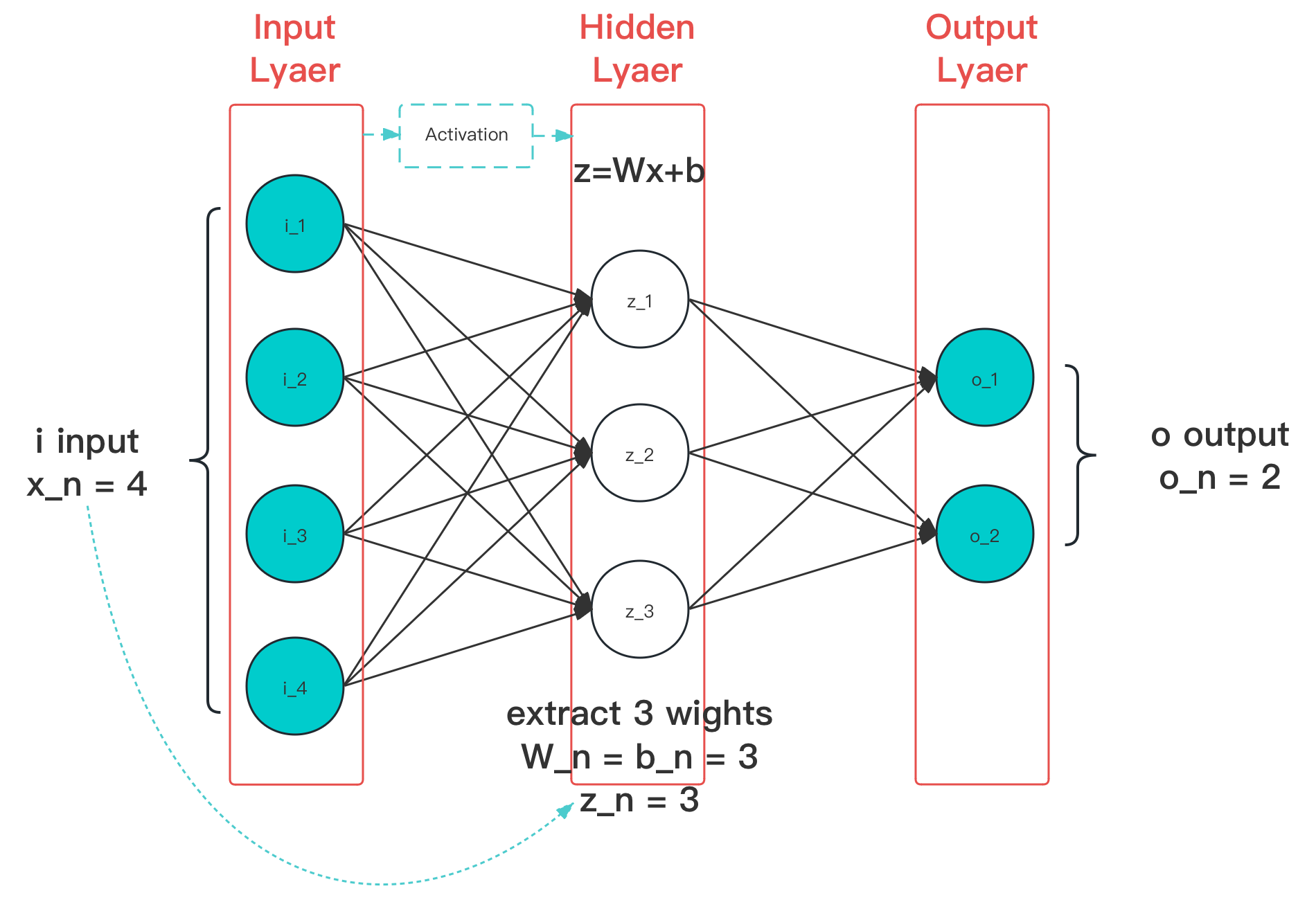
图 4-8 激活函数作用阶段(图中蓝色线条)示意图
从图上可以看出,激活函数主要作用于隐藏层的输入。示例中只有一层隐藏层,因此激活函数作用位置在输入层接收输入数据后,交付到隐藏层的过程中。而对于多个隐藏层情况,前一级的输入也会经激活后才交付给后一级。
如果不采用激活函数,那么我们经过每层神经网络计算后,得到的最终输出都将为线性结果。线性输出实际就是最原始的感知器(Perceptron)。而单纯使用线性函数计算,在实际的处理过程中,对于大多是场景将不能很好的描述其特征。常见的算法问题常常需要引入非线性特性,才能更好的拟合样本。通常,我们通过引入激活函数来给我们设计、使用的神经网络,提供逼近任何非线性场景的能力。
激活函数,基本满足:单一输入输出、单一层处理、可参与训练参数 ,的一类激活函数。其中常用的几类,被称为 经典激活函数(Classic Activation Function)。
一般的:
- 当一个激活函数 满足 时,我们称之为 右饱和。
- 当一个激活函数 满足 时,我们称之为 左饱和。
- 当一个激活函数,既满足左饱和又满足又饱和时,我们称之为 饱和。
- 对任意的 ,如果存在常数 ,当 时恒有 取值,则称其为 右硬饱和。
- 对任意的 ,如果存在常数 ,当 时恒有 取值,则称其为 左硬饱和。
- 若既满足左硬饱和,又满足右硬饱和,则称这种激活函数为 硬饱和。
- 如果只有在 极限 状态下偏导数 的函数,称之为 软饱和。
由于激活函数的作用,大多基于同向对比实验的统计结果来进行说明(目前,部分有相关的数理研究佐证,如 ReLU,但仍有争议)。因此,这里仅列出算子的公认已证明特性,和 C 语言实现。