4.3.4 ReLU 族
矫正线性单元(ReLU [Rectified Linear Unit]) 是整个经典激活函数中,被使用最广泛的经典中的经典。经过多年探索,已经形成了一系列以 ReLU 为基础的多种变体,用于各种突出场景。
ReLU(Rectified Linear Unit)
迭代公式:
图像:
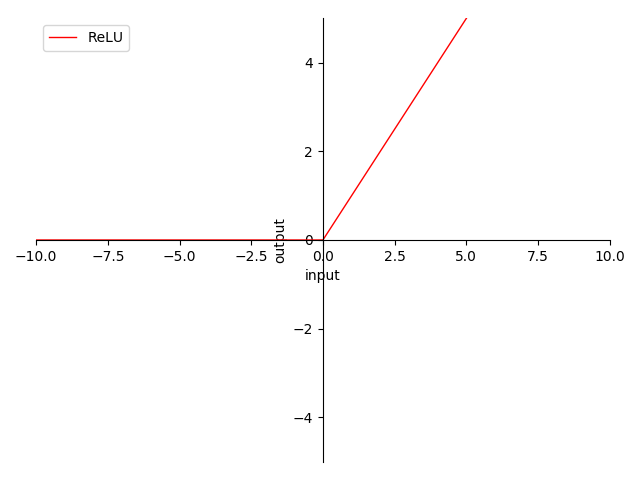
图 4-12 ReLU 函数图
特性:
- 非 0 为中心(non-zero-centered)
- 输出范围在 之间
- 输出 ,反向传播(BP)权值正向堆积(梯度始终 )
- 当输入在 时,梯度为常量 ,完美解决梯度消失问题 及 梯度爆炸问题
- 当输入在 时,梯度为 ,面临梯度归零问题
- 线性处理便于计算
ReLU(2013)被称为 线性整流函数,又称为线性修正单元。ReLU 因其简洁的特性,极低的运算量,成为了当前最常用的激活函数。业界各位炼丹师在不清楚或不确定具体使用什么激活函数时,常常选择 ReLU 或 其变体 来作为默认激活函数。
不过,纯粹的 ReLU 因为对于 < 0 的输入是没有定义导数的。这会导致,当输入特性 < 0 使得输出为 0,那么对应的权重将在后续过程中再也无法激活,导致 神经元死亡(Dead Neuron)。已经不是梯度消失,而是直接没有了哪怕细微的迭代变化可能,即完全失活梯度归零。
但即便如此,ReLU 仍是目前最好用的激活函数。
PReLU & LReLU & RReLU
迭代公式:
图像:
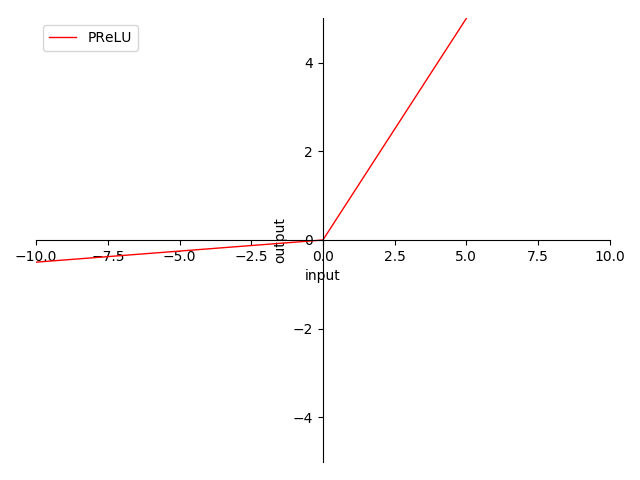
图 4-13 PReLU & LReLU & RReLU 函数图
特性:
- 0 为中心(zero-centered)
- 输出范围在 之间
- 输出值域对称,降低在正向堆积风险
- 当输入在 时,梯度为常量 ,完美解决梯度消失问题 及 梯度爆炸问题
- 当输入在 时,PReLU 梯度为训练参数 (参与训练,启动值为 )
- 当输入在 时,LReLU 梯度为 (常量)
- 当输入在 时,RReLU 梯度为范围内参数(随机值)
- 当输入在 时,三类梯度度 (大部分情况),还是存在 梯度消失问题
- 线性处理便于计算
PReLU(2016) 、 LReLU(2015 Russakovsky ImageNet 分类)、RReLU(2017 Kaggle 全美数据科学大赛 即 NDSB) 三者间的差别主要就在于 ( 0, +∞) 时的梯度是常数、参与训练、随机限定范围内取值。三者的目的都是试图通过引入 < 0 时的输出导数,来处理梯度消失导致的神经元死亡问题,同时也通过引入负值来处理可能的梯度爆炸问题。这三个都是目前最为常用的激活函数(尤其是 LReLU),收敛速度快、错误率低,且没有明显缺点。
ReLU 灵活方案:NReLU(Noisy ReLU)& ReLU-N
除了上述的 ReLU 变体外,我们还可以根据实际需要选择在使用上述变体的时候,引入辅助处理,常见的辅助处理有两种:
- 当输入在 时,引入噪音偏置常量(梯度非 ),或参与训练参数(类 PReLU)
- 当输入在 时,限定最大上限常量(右饱和),或类比 LReLU 处理
这样的操作常用在一些需要限定约束激活层输出的地方使用,属于 小技巧(Tricks)。是需要 谨慎使用 的一种处理手段。
ReLU 族算子化
利用 C 语言实现对算子的封装,有:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double relu(double x) {
return fmax(0, x);
}
double prelu(double x, double tau) {
return fmax(0, x) + tau * fmin(0, x);
}
double lrelu(double x, double alpha) {
return fmax(alpha * x, x);
}
double rrelu(double x, double alpha, double lower, double upper) {
double r = (double)rand() / (double)RAND_MAX;
double alpha_rand = lower + r * (upper - lower);
return fmax(alpha_rand * x, x);
}
int main() {
// ReLU
{
double x = -0.5;
double y = relu(x);
printf("The ReLU of %f is %f\n", x, y);
}
{
double x = +0.5;
double y = relu(x);
printf("The ReLU of %f is %f\n", x, y);
}
// PReLU
{
double x = -0.5;
double tau = 0.1;
double y = prelu(x, tau);
printf("The PReLU of %f with alpha=%f is %f\n", x, tau, y);
}
// LReLU
{
double x = -0.5;
double alpha = 0.1;
double y = lrelu(x, alpha);
printf("The LReLU of %f with alpha=%f is %f\n", x, alpha, y);
}
// RReLU
{
// Set the random seed
srand(time(NULL));
double x = -0.5;
double alpha = 0.1;
double lower = 0.0;
double upper = 1.0;
double y = rrelu(x, alpha, lower, upper);
printf("The RReLU of %f with alpha=%f, lower=%f, and upper=%f is %f\n", x,
alpha, lower, upper, y);
}
return 0;
}
运行验证可得到结果:
The ReLU of -0.500000 is 0.000000
The ReLU of +0.500000 is 0.500000
The PReLU of -0.500000 with alpha=0.100000 is -0.050000
The LReLU of -0.500000 with alpha=0.100000 is -0.050000
The RReLU of -0.500000 with alpha=0.100000, lower=0.000000, and upper=1.000000 is -0.019595